Question

How do you write the point slope of the equation given $\left( 1,-3 \right)$ and parallel to $0$ ?

Answer 1

Hint: There are many different forms of only one line. There is slope intercept form, point slope, parametric equation of a line. At the end, different equations of a line talk about the same line. So, here, we are going to specifically look at the point slope form of the line. The general equation of a point slope form is $y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$ , where $m$ is the slope of the line and $\left( {{x}_{1}},{{y}_{1}} \right)$ is a point on the line. In this question, we are already given our slope$\left( m \right)$ which is $0$.

Complete step by step solution:
Since, we already have our slope$\left( m \right)$, and a point which satisfies that line, represented by $\left( {{x}_{1}},{{y}_{1}} \right)$, we are supposed to find out is already given which is $\left( -2,4 \right)$.
Let us substitute all that we have in the standard equation of slope point form of a line which is $y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$.
Upon substituting, we get the following :
\[\begin{align}
  & \Rightarrow y-{{y}_{1}}=m\left( x-{{x}_{1}} \right) \\
 & \Rightarrow y-\left( -3 \right)=0\left( x-1 \right) \\
\end{align}\]
Let us solve further to get the equation of our line.
\[\begin{align}
  & \Rightarrow y-{{y}_{1}}=m\left( x-{{x}_{1}} \right) \\
 & \Rightarrow y-\left( -3 \right)=0\left( x-1 \right) \\
 & \Rightarrow y+3=0 \\
 & \Rightarrow y=-3 \\
\end{align}\]
$\therefore $ \[y=-3\]is the slope point equation of the line which has the point $\left( 1,-3 \right)$ and has a slope of $0$.
Graph for reference :

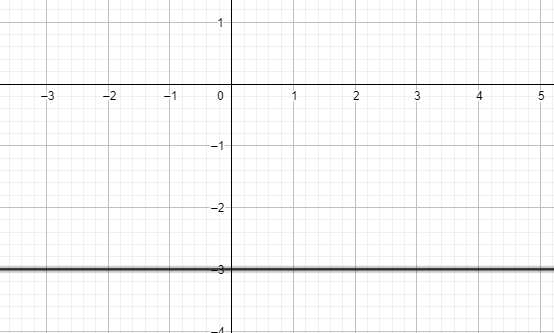
Note: We notice that we got a line which is parallel to $x$ -axis. So we can remember from nor onwards that a line with $0$ slope is always parallel to $x$ -axis. It is important to remember all the general forms of a line and their standard equation so as to complete a question quickly and accurately in the exam. We should also know the conditions when two lines are parallel or when two lines are said to be perpendicular. We should also be careful while substituting the values.