
How do you write the factor trees for $24$ ?
Answer
562.8k+ views
Hint: Whenever they ask to draw the factor tree for any number the number should be a non-prime number. First, find the two factors of the given number so that one of them is not prime. Again the non-prime number should be factored further until we get a prime number that cannot be divided further, which gives us the factor tree.
Complete step by step answer:
In this question, they have asked us to write the factor tree for the number $24$. In order to write the factor tree first, we need to find the prime factors that divide the given number. Primes numbers are those numbers that can be divided only by one and the number itself. For example 2, 3, 5, 7, and so on.
A factor tree is nothing but it represents a tree structure where the factors are represented like leaves in the tree.
First, we need to find the two factors of the given number $24$ so that one of them should be at least a non-prime number.
The given number $24$ which is not a prime number divided by $2$ a prime number, therefore factor tree is written as below,
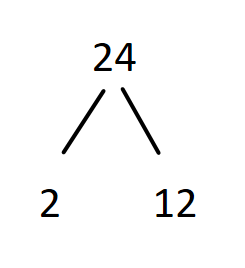
Again the number $12$ which is not a prime number can be divided further by the prime number $2$, therefore we get
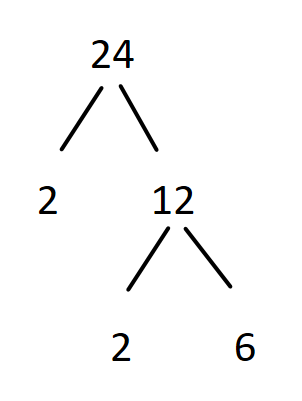
Again the $6$ which is not a prime number can be divided by $2$, we get
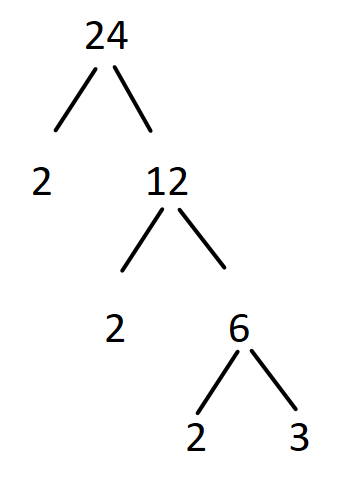
Now, we don’t have any non-prime number to divide further, so the factor tree for the number $24$ is as shown in the above diagram.
Hence the prime factors can be written as $24 = 2 \times 2 \times 2 \times 3$ or $24 = {2^3} \times 3$.
Note:
Whenever they ask to write the factor tree for any given number first you need to find the prime factors of that number until you get all the factors as prime numbers. Once you get all the factors as the prime number you can represent those in terms of the tree structure as in the above problem. Here the prime factors represent the leaves in the tree.
Complete step by step answer:
In this question, they have asked us to write the factor tree for the number $24$. In order to write the factor tree first, we need to find the prime factors that divide the given number. Primes numbers are those numbers that can be divided only by one and the number itself. For example 2, 3, 5, 7, and so on.
A factor tree is nothing but it represents a tree structure where the factors are represented like leaves in the tree.
First, we need to find the two factors of the given number $24$ so that one of them should be at least a non-prime number.
The given number $24$ which is not a prime number divided by $2$ a prime number, therefore factor tree is written as below,
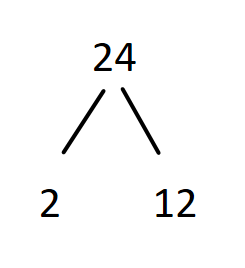
Again the number $12$ which is not a prime number can be divided further by the prime number $2$, therefore we get
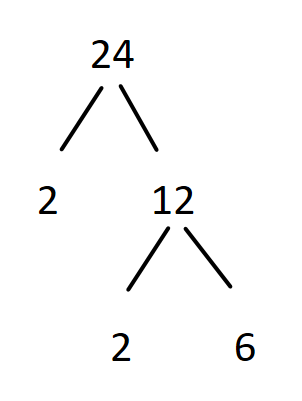
Again the $6$ which is not a prime number can be divided by $2$, we get

Now, we don’t have any non-prime number to divide further, so the factor tree for the number $24$ is as shown in the above diagram.
Hence the prime factors can be written as $24 = 2 \times 2 \times 2 \times 3$ or $24 = {2^3} \times 3$.
Note:
Whenever they ask to write the factor tree for any given number first you need to find the prime factors of that number until you get all the factors as prime numbers. Once you get all the factors as the prime number you can represent those in terms of the tree structure as in the above problem. Here the prime factors represent the leaves in the tree.
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Trending doubts
What is the capital city of Australia? A) Sydney B) Melbourne C) Brisbane D) Canberra

Give 10 examples for herbs , shrubs , climbers , creepers

What is the shape of Earth A Circle B Square C Sphere class 6 social science CBSE

Draw a diagram of nephron and explain its structur class 11 biology CBSE

Explain zero factorial class 11 maths CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE





