Question

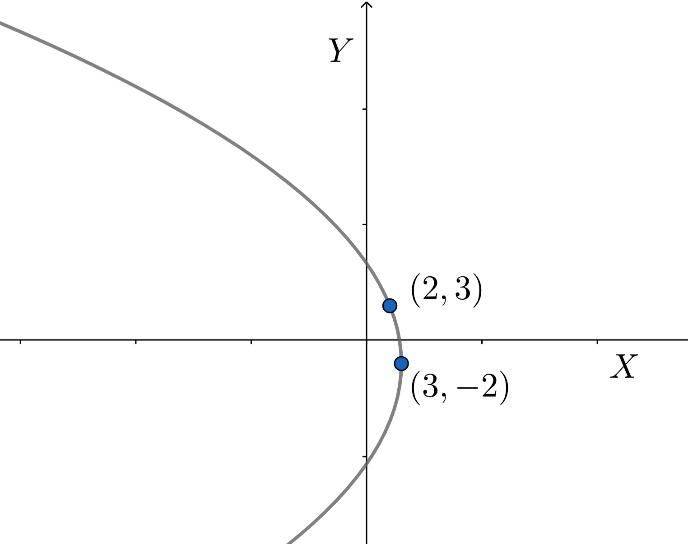
How do you write the equation of the parabola in vertex form given vertex \[\left( 3,-2 \right)\] , point \[\left( 2,3 \right)\] ?

Answer 1

Hint: The above given problem is a very simple problem of coordinate geometry. The sub-topic is parabola, and for solving such problems we need to first understand what the different forms of parabolas are possible. There are four general types of parabola and for each of them, the corresponding vertex and foci are as follows,

Equation	Vertex	Foci
\[{{y}^{2}}=4ax\]	\[\left( 0,0 \right)\]	\[\left( a,0 \right)\]
\[{{y}^{2}}=-4ax\]	\[\left( 0,0 \right)\]	\[\left( -a,0 \right)\]
\[{{x}^{2}}=4by\]	\[\left( 0,0 \right)\]	\[\left( 0,b \right)\]
\[{{x}^{2}}=-4by\]	\[\left( 0,0 \right)\]	\[\left( 0,-b \right)\]

Complete step-by-step solution:
Now the most generalised form of parabola that we can represent, given that we have the vertex of the parabola and the latus rectum is \[{{\left( y-k \right)}^{2}}=4a\left( x-h \right)\] . Here in this equation, we have, \[\left( h,k \right)\] as the vertex of the parabola and ‘4a’ as the length of the latus rectum. However if we are given a vertex point and any other point, then also we can very easily find out the equation of the parabola by putting the point in the generalized equation of the parabola to find out the length of the latus rectum.
Now we start off with the solution of the given problem by putting the vertex points on the generalised equation of the parabola, and hence it transforms to,
\[\begin{align}
  & {{\left( y-k \right)}^{2}}=4a\left( x-h \right) \\
 & \Rightarrow {{\left( y+2 \right)}^{2}}=4a\left( x-3 \right) \\
\end{align}\]
Now in this equation we put the given point to find the value of the latus rectum. Thus we do,
\[\begin{align}
  & {{\left( y+2 \right)}^{2}}=4a\left( x-3 \right) \\
 & \Rightarrow {{\left( 3+2 \right)}^{2}}=4a\left( 2-3 \right) \\
 & \Rightarrow 4a=\dfrac{25}{-1} \\
 & \Rightarrow 4a=-25 \\
\end{align}\]
Now we put this found out value in our original equation to from the required equation of the parabola,
\[{{\left( y+2 \right)}^{2}}=-25\left( x-3 \right)\]
This equation of the parabola is thus our required answer.

Note: Problems related to parabola or any other conic section are very easy to solve once we know about the formulae and other equations related to it. In this problem we first need to assume the equation of the parabola and then by putting the given points we find out all the unknowns. Putting all the values of the unknowns in our assumed equation we thus find out our required equation of the parabola.