Question

How do you write the equation of circle with center $ \left( 2,4 \right) $ and containing the point $ \left( -2,1 \right) $ ?

Answer 1

Hint: All points on a circle are equidistant from the center of the circle. Radius is the distance between center and any point on the circle. So we can find out the radius of the circle as we have the coordinates of center and a point on the circle. We have the radius and center of the circle these 2 things are enough to write the equation of a circle.

Complete step by step answer:
The center of given circle= $ \left( 2,4 \right) $
Circle contains the point $ \left( -2,1 \right) $ .
 The distance between center of circle and any point on the circle is the radius. So the distance between $ \left( 2,4 \right) $ and $ \left( -2,1 \right) $
Applying distance formula $ \sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}} $
 $ =\sqrt{{{\left( 2-\left( -2 \right) \right)}^{2}}+{{\left( 4-1 \right)}^{2}}} $
Further solving
 $ \Rightarrow \sqrt{{{\left( 2-\left( -2 \right) \right)}^{2}}+{{\left( 4-1 \right)}^{2}}}=\sqrt{16+9} $
 $ =5 $
So the we get the radius of circle equal to 5 units.
We know that the collection of all points at equal distance from a fixed point forms a circle. The fixed point is the center of the circle. The fixed distance is the radius of the circle.
Let us assume the coordinate of center of circle is $ \left( \alpha ,\beta \right) $ and radius is r then the locus of all point at distance of r units from $ \left( \alpha ,\beta \right) $ would be $ \sqrt{{{\left( x-\alpha \right)}^{2}}+{{\left( y-\beta \right)}^{2}}}=r $
Further solving the equation squaring both sides
 $ \Rightarrow {{\left( x-\alpha \right)}^{2}}+{{\left( y-\beta \right)}^{2}}={{r}^{2}} $
So the equation of circle having center $ \left( \alpha ,\beta \right) $ and radius r is $ {{\left( x-\alpha \right)}^{2}}+{{\left( y-\beta \right)}^{2}}={{r}^{2}} $
Our center is $ \left( 2,4 \right) $ and radius is 5 so the equation will be
 $ {{\left( x-2 \right)}^{2}}+{{\left( y-4 \right)}^{2}}=25 $
Further solving the equation we get
 $ {{x}^{2}}+{{y}^{2}}-4x-8y-5=0 $
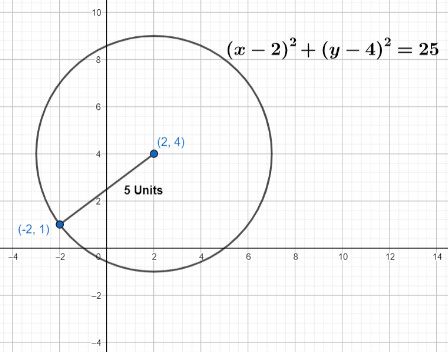
Now we can draw the graph

Note:
 The equation of circle generally written in the format $ {{\left( x-\alpha \right)}^{2}}+{{\left( y-\beta \right)}^{2}}={{r}^{2}} $ sometime it is written as $ {{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0 $ in this equation the center of circle is $ \left( -g,-f \right) $ and the radius $ r=\sqrt{{{g}^{2}}+{{f}^{2}}-c} $ so here we can see that $ {{g}^{2}}+{{f}^{2}} $ should be greater than $ c $ otherwise the equation will not form a circle. Always remember that in the equation of circle, coefficient of $ {{x}^{2}} $ and $ {{y}^{2}} $ is always same.