Question

How do you write $ f\left( x \right)={{x}^{2}}+6x+12 $ in vertex form?

Answer 1

Hint: We will look at the general equation representing the vertex form of a quadratic equation. Then we will use the completing square method. We will shift the constant term to one side and the $ {{x}^{2}} $ and $ x $ terms on the other side. Then we will add a perfect square to both sides of the equation and simplify it to obtain the vertex form of the quadratic equation.

Complete step by step answer:
The general equation representing the vertex form of a quadratic equation is given as
 $ f\left( x \right)=a{{\left( x-h \right)}^{2}}+k $
where $ \left( h,k \right) $ is the vertex.
The given quadratic equation is $ f\left( x \right)={{x}^{2}}+6x+12 $ . We will be using the completing square method to convert this equation into its vertex form. For that, we will first shift the constant term to the other side of the equation. So, we get the following equation,
 $ f\left( x \right)-12={{x}^{2}}+6x....(i) $
Now, for completing the square on the right hand side of the above equation, we will add a perfect square to both sides of the equation. This perfect square will be calculated in the following manner,
 $ \text{perfect square to be added}={{\left( \dfrac{1}{2}\times \text{coefficient of }x \right)}^{2}} $
The coefficient of $ x $ is 6. Substituting this value in the above formula, we get
 $ \begin{align}
  & \text{perfect square to be added}={{\left( \dfrac{1}{2}\times 6 \right)}^{2}} \\
 & \Rightarrow \text{perfect square to be added}={{\left( 3 \right)}^{2}} \\
 & \therefore \text{perfect square to be added}=9 \\
\end{align} $
Now, we will add this perfect square on both the sides of equation $ (i) $ in the following manner,
 $ f\left( x \right)-12+9={{x}^{2}}+6x+9 $
We can simplify the right hand side of the above equation using the identity $ {{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}} $ . After simplification, we get the following,
 $ f\left( x \right)-3={{\left( x+3 \right)}^{2}} $
Shifting the constant term back to the right hand side, we get the vertex form of the given quadratic equation. The vertex form of the quadratic equation is $ f\left( x \right)={{\left( x+3 \right)}^{2}}+3 $ and the vertex is $ \left( -3,3 \right) $ . The graph looks like the following,

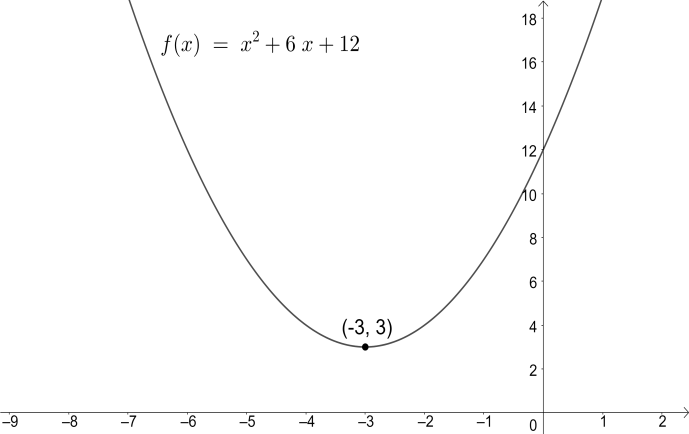
Note:
The vertex is the vertex of the parabola represented by the quadratic equation. The graph of a quadratic equation is always a parabola. We should be familiar with the methods of solving quadratic equations. These methods are factorization, completing the square, using the quadratic formula.