Question

How do you write $f\left( x \right)=\left| x-4 \right|$ in piecewise function?

Answer 1

Hint: We know that the function |x| is symmetric with respect to Y axis or x= 0 that means if we move to x units towards right of Y axis then the value of function |x| will be equal if we move to x units towards the left of Y axis. Similarly |x- m| is symmetric with respect to the line
 x= m. Whatever the function inside the mod it will remain the same if the value of the function is greater than 0, if the value of the function inside mod is negative then we just multiply the value with -1.

Complete step by step answer:
Let’s convert $f\left( x \right)=\left| x-4 \right|$ into piecewise function
We know that |x| will be equal to x when x is greater than equal to 0 and |x| will be – x when x is less than 0
 Now we can write
$\left| x-4 \right|=x-4$ when $x-4\ge 0$ or $x\ge 4$
$\left| x-4 \right|=4-x$ when $x-4<0$ or $x<4$
When we draw the graph of $\left| x-4 \right|$ we can draw x - 4 when x is greater than equal to 4 and 4 - x when x is less than 4.

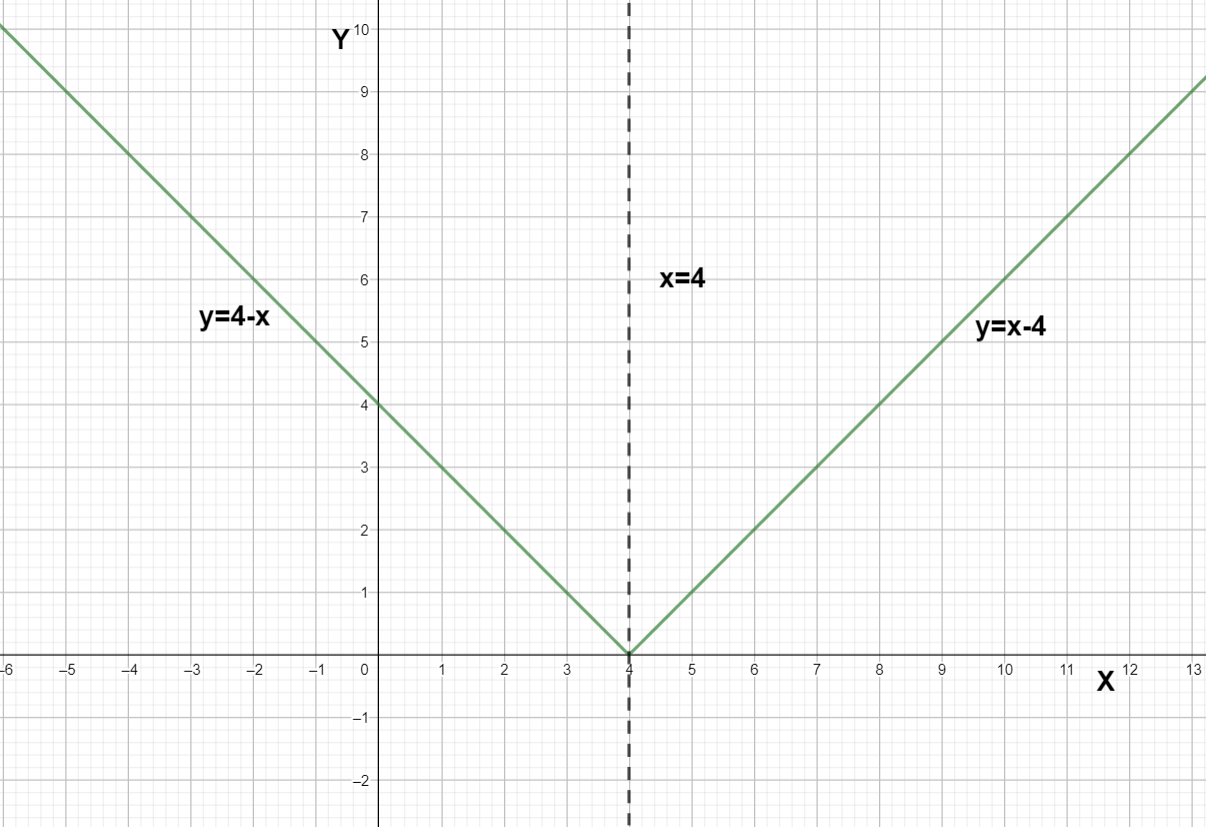
We can see the graph of $f\left( x \right)=\left| x-4 \right|$ is symmetric with respect to x = 4

Note:
If we draw the graph of f(x) and shift the graph k units towards right then we will get the graph of f(x – k) similar if we shift the graph k units towards left we will get the graph of f(x +k)
We can see that the if we shift the graph |x| k units towards right we will get graph of |x-4|