Question

Write down the equation of the line AB through (3, 2), parallel to the line $ 3x - 2y + 5 = 0 $ . AB meets x-axis at A and y-axis at B. Calculate the area of the triangle OAB when O is the origin.

Answer 1

Hint: Parallel lines will have the same slope. So, find the slope of the given equation (linear) from the question by converting the equation into slope-intercept form. The resulting slope is the slope for the required equation too. Substitute the slope value and coordinates (3, 2) in the point-slope form to get the new line equation. Convert the obtained line equation to x-intercept and y-intercept format (intercept form) and we will get the x and y coordinates which is the base and the height of the triangle OAB. Find the area of the triangle using formula by substituting its base and height.

Complete step-by-step answer:
We are given that the line AB is parallel to the line $ 3x - 2y + 5 = 0 $ and line AB passes through the point (3, 2). AB meets the x-axis at A and y-axis at B which means the y-coordinate of point A is zero and x-coordinate of point B is zero.
A= (x, 0); B= (0, y)
Convert the equation $ 3x - 2y + 5 = 0 $ into slope -intercept form $ y = mx + c $
  $
  3x - 2y + 5 = 0 \\
  3x + 5 = 2y \\
  2y = 3x + 5 \\
  y = \dfrac{{3x + 5}}{2} \\
  y = \dfrac{{3x}}{2} + \dfrac{5}{2} \\
  y = \dfrac{3}{2}x + \dfrac{5}{2} \\
  $
Comparing the above obtained equation with $ y = mx + c $ , we get $ m = \dfrac{3}{2},c = \dfrac{5}{2} $
Therefore, the slope of the required equation is $ \dfrac{3}{2} $ .
Substitute the slope and the point (3, 2) in the point-slope form of an equation $ y - {y_1} = m\left( {x - {x_1}} \right) $ to get the desired equation.
  $
  m = \dfrac{3}{2},\left( {{x_1},{y_1}} \right) = \left( {3,2} \right) \\
   \to y - {y_1} = m\left( {x - {x_1}} \right) \\
   \to y - 2 = \dfrac{3}{2}\left( {x - 3} \right) \\
   \to 2\left( {y - 2} \right) = 3\left( {x - 3} \right) \\
   \to 2y - 4 = 3x - 9 \\
   \to 3x - 9 - 2y + 4 = 0 \\
   \to 3x - 2y - 5 = 0 \\
  $
Therefore, the new line equation if $ 3x - 2y - 5 = 0 $
Convert the above equation into intercept form which is $ \dfrac{x}{a} + \dfrac{y}{b} = 1 $
  $ 3x - 2y = 5 $
Divide both sides by 5
  $
  \dfrac{{3x - 2y}}{5} = \dfrac{5}{5} \\
  \dfrac{{3x}}{5} - \dfrac{{2y}}{5} = 1 \\
  \dfrac{x}{{\left( {\dfrac{5}{3}} \right)}} - \dfrac{y}{{\left( {\dfrac{5}{2}} \right)}} = 1 \\
  \dfrac{x}{{\left( {\dfrac{5}{3}} \right)}} + \dfrac{y}{{\left( { - \dfrac{5}{2}} \right)}} = 1 \\
    \\
  $
By comparing the above equation with $ \dfrac{x}{a} + \dfrac{y}{b} = 1 $
We get $ a = \dfrac{5}{3},b = - \dfrac{5}{2} $
Which means the x-coordinate of point A, y-coordinate of point B is $ \dfrac{5}{3}, - \dfrac{5}{2} $ respectively.
 

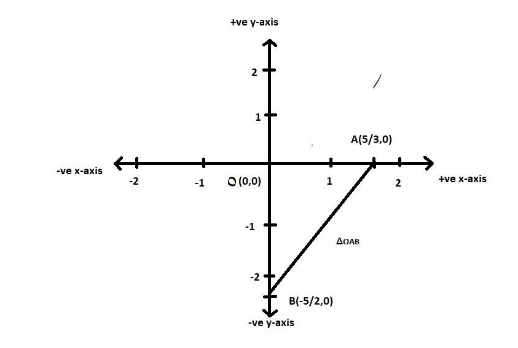
From the above diagram, we can see the triangle OAB with base OA and height OB
 $ OA = \dfrac{5}{3},OB = - \dfrac{5}{2} $
Area of the triangle is $ \dfrac{1}{2} \times b \times h $
  $
  b = \dfrac{5}{3},h = - \dfrac{5}{2} \\
   = \dfrac{1}{2} \times \dfrac{5}{3} \times \left| {\dfrac{{ - 5}}{2}} \right| \\
   = \dfrac{{25}}{{12}}sq.units \\
  $
As the area cannot be negative considered all the negative values as positive
Therefore, the area of triangle OAB where O is the origin is $ \dfrac{{25}}{{12}}sq.units $

Note: Do not confuse the different forms of line equations. Other types of line equations are Standard form, Two points form, Vertical form, Horizontal form etc.
Slope-intercept form of a linear equation $ y = mx + c $ where c is the y-intercept and ‘m’ is the slope.
Point-slope form of an equation is $ y - {y_1} = m\left( {x - {x_1}} \right) $
Intercept form of an equation is $ \dfrac{x}{a} + \dfrac{y}{b} = 1 $ where ‘a’ is the x-intercept and ‘b’ is the y-intercept.
Area of a triangle when base ’b’ and height ‘h’ is given is $ \dfrac{1}{2} \times b \times h $