Question

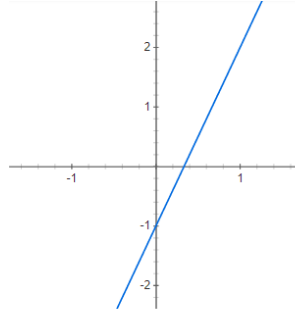
Write down the equation of line below in image. Give your answer in the form y = mx + c.

Answer 1

Hint: We will just find out two points in the graph which the line is passing through. After finding those points, put in those points in the equation y = mx + c. Now, we will get the values of m and c on solving and thus the required equation of line.

Complete step-by-step answer:
Let us first assume the equation of the line by y = mx + c.
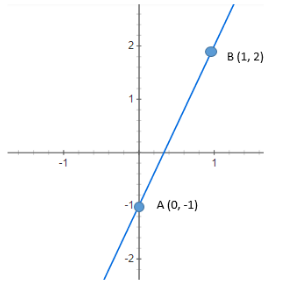
Let us clearly look at the image below and the points A and B which lie on the line whose equation we
require to find.
So, we see that the line passes through A and B, where A = (0, -1) and B = (1, 2).
Now, we can clearly see that the line is passing through A (0, -1) and B (1, 2).

We will now put in the first point in the equation y = mx + c.
\[\therefore \] let us put in x = 0 and y = -1 in this.
We will get:
$ \Rightarrow - 1 = m(0) + c$
Simplifying the m.0 part, we will get:-
$ \Rightarrow c = - 1$
\[\therefore \] the equation of the line becomes y = mx – 1.
Now, let us put in another point B in this.
\[\therefore \] let us put in x = 1 and y = 2 in y = mx – 1. We will get:-
$ \Rightarrow 2 = m(1) - 1$
Simplifying the RHS, we will get:-
$ \Rightarrow 2 = m - 1$
Taking 1 from subtraction in RHS to addition in LHS, we will get:-
$ \Rightarrow m = 3$

\[\therefore \] The equation of the line becomes y = 3x – 1.

Note: The students must note that here we had to form two equations because we had two unknown variables m and c. We need as many equations as many unknown variables we need to find. Though x and y are variables as well. We can find infinite equations of lines using one point but we can find a unique equation of line with 2 points. And, if we have 3 points or more, we will not be able to find the equation of the lie if the points are non-collinear.