Question

How do I work with the exponential model $y=a{e}^{kt}$ ?

Answer 1

Hint: When we have to work with an exponential model $y=a{e}^{kt}$ , we have to consider two cases, one with ‘k’ greater that zero and another with ‘k’ less than zero. We must know its initial values and the asymptotic equation.

Complete step-by-step answer:
It is given that a function,
 $y=a{e}^{kt}$
For exponential growth ,
We have to consider $$k>0$$ ,
For this we have certain features given as follows:
It is asymptotic to $y=0$ to the left.
It will pass through $(0,1)$ .
The initial value is one.
Graph will increase without bound to the right.

There exist some of the things where we used exponential growth include population growth model, bacterial growth model, and compound interest model.
And for exponential decay we have,
 $y=a{e}^{kt}$
We have to consider $$k<0$$ for decay ,
For this we have certain features given as follows:
It is asymptotic to $y=0$ to the right.
It will pass through $(0,1)$ .
The initial value is one.
Graph will be decreasing , it bounded below by $y=0$ .

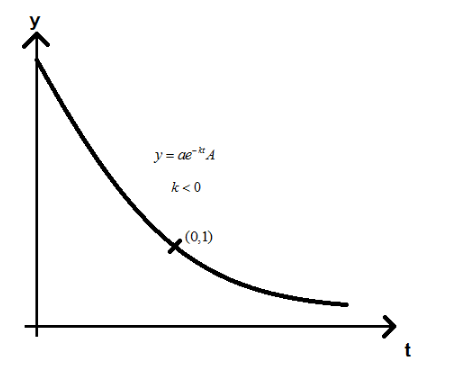
There exist some of the things where we used exponential decay including the radioactive decay model and the depreciation model.

Note: If the initial value is given to you , that is the value to get when you put $x=0$ , the value you get in known as the constant ‘C’ or the initial value of the exponential function. If you know the initial value of the exponential function then the rest of the model is fairly easy to complete.