Question

Work done by a centripetal force:
(A) Increase by decrease in radius of the circle.
(B) Decrease by increasing the radius of the circle.
(C) Increase by increasing mass of the body.
(D) Is always zero.

Answer 1

Hint :To solve this problem we should know about the basic concept of work.
Work: when force is applied on an object and it is displaced from its position in any direction. Then we can say that some work has been done.
Mathematically work will be written as: $ W = F.d = Fd\cos \theta $ .
Here, $ \theta $ is the angle between the force vector and the displacement vector.
Centripetal force: A force acting on a body to keep it moving in a circular path.

Complete Step By Step Answer:
As we know that the centripetal force causes the body to rotate in circular orbit and it acts in outward direction and displacement will be in perpendicular direction to the centripetal force.

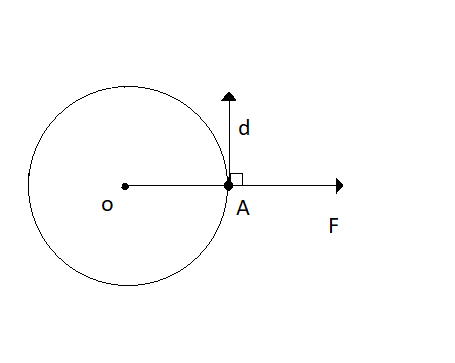
As given in the figure $ F $ is centripetal force and $ d $ is displacement of the object.
As we can see from the figure, the angle between direction force and displacement will be $ \theta = {90^ \circ } $ .
From the formula of force:
  $ W = F.d = Fd\cos \theta $
We get,
  $ \Rightarrow W = Fd\cos {90^ \circ } $
  $ \Rightarrow W = 0 $
Hence we can observe from the above the work done by centripetal force will always be zero.
So, option (d) will be correct.

Note :
Force: A force is push and pull act upon an object which causes change in speed, direction or shape. It can be positive, negative or zero.
Displacement: the dislocation of an object from its mean position in any direction with respect to its mean position. It can be negative, positive or zero. But we know that distance can never be a negative quantity.
Centripetal force only came into existence only when circular motion existed.