Question

With the usual notation, in \[\Delta ABC\], if \[\angle A + \angle B = 120^\circ ,a = \sqrt 3 + 1\] and \[b = \sqrt 3 - 1\]. Then, what will be the ratio for \[\angle A:\angle B\] ?

Answer 1

Hint: This question is from Trigonometric geometry. We have to know the angle property for any triangle will be \[\angle A + \angle B + \angle C = 180^\circ \]. By using sine rule property for triangle ABC, we have to show \[\dfrac{{a - b}}{{a + b}}\cot \dfrac{C}{2} = \tan \left( {\dfrac{{A - B}}{2}} \right)\]. Then, by putting given values of a and b in this equation we will get \[\angle A:\angle B\]

Complete step-by-step answer:

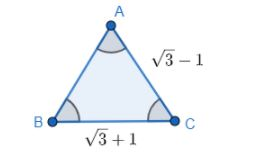
Given, \[\angle A + \angle B = 120^\circ {\rm{ }}...{\rm{(i)}}\]
\[\begin{array}{l}

{\rm{In }}\Delta {\rm{ABC, by using Sine Rule,we get}}\\
\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = k
\end{array}\]
Now, we can write equation for a, b and c
\[a = k\sin A,b = k\sin C,c = k\sin C\]
Now, we have
\[ \Rightarrow \dfrac{{a - b}}{{a + b}}\cot \dfrac{C}{2}\]
We can write values of a, b and c in this equation
\[ = \left( {\dfrac{{k\sin A - k\sin B}}{{k\sin A + k\sin B}}} \right)\cot \dfrac{C}{2}\]
We can expand this equation as follows,
\[ = \dfrac{{2\cos \left( {\dfrac{{A + B}}{2}} \right).\sin \left( {\dfrac{{A - B}}{2}} \right)}}{{2\sin \left( {\dfrac{{A + B}}{2}} \right).\cos \left( {\dfrac{{A - B}}{2}} \right)}}.\dfrac{{\cos \left( {\dfrac{C}{2}} \right)}}{{\sin \left( {\dfrac{C}{2}} \right)}}\]
But, we know
\[\begin{array}{l}
A + B + C = \pi \\
A + B = \pi - C
\end{array}\]
Now, we can put values of A + B in this equation
\[ \Rightarrow \dfrac{{\cos \left( {\dfrac{\pi }{2} - \dfrac{C}{2}} \right).\sin \left( {\dfrac{{A - B}}{2}} \right)}}{{\sin \left( {\dfrac{\pi }{2} - \dfrac{C}{2}} \right).\cos \left( {\dfrac{{A - B}}{2}} \right)}} \times \dfrac{{\cos \left( {\dfrac{C}{2}} \right)}}{{\sin \left( {\dfrac{C}{2}} \right)}}\]
On simplification, we get
\[ \Rightarrow \dfrac{{\sin \left( {\dfrac{C}{2}} \right)}}{{\sin \left( {\dfrac{C}{2}} \right)}} \times \tan \left( {\dfrac{{A - B}}{2}} \right) \times \dfrac{{\cos \left( {\dfrac{C}{2}} \right)}}{{\sin \left( {\dfrac{C}{2}} \right)}}\]
\[ \Rightarrow \tan \left( {\dfrac{{A - B}}{2}} \right)\]
Hence, we get
\[ \Rightarrow \dfrac{{a - b}}{{a + b}}\cot \dfrac{C}{2} = \tan \left( {\dfrac{{A - B}}{2}} \right)\]
Now, \[\tan \left( {\dfrac{{A - B}}{2}} \right) = \dfrac{{a - b}}{{a + b}}\cot \left( {\dfrac{C}{2}} \right)\]
We can put given values of a = and b = in this equation.
\[ = \dfrac{{\sqrt 3 + 1 - \sqrt 3 + 1}}{{2\left( {\sqrt 3 } \right)}}\cot \left( {\dfrac{{60^\circ }}{2}} \right)\]
\[\left[ \begin{array}{l}
{\rm{As }}A + B + C = 180^\circ \\
\angle C = 180^\circ - 120^\circ = 60^\circ
\end{array} \right]\]
\[ = \dfrac{{\sqrt 3 + 1 - \sqrt 3 + 1}}{{2\left( {\sqrt 3 } \right)}}\cot \left( {30^\circ } \right)\]
On simplification, we get
\[ = \dfrac{1}{{\sqrt 3 }}.\sqrt 3 = 1\]
\[ \Rightarrow \tan \left( {\dfrac{{A - B}}{2}} \right) = 1\]
Now, we can convert this equation as,
\[\dfrac{{A - B}}{2} = {\tan ^{ - 1}}\left( 1 \right)\]
But, we know,
\[{\tan ^{ - 1}}\left( 1 \right) = 45^\circ \]
Now, equation becomes
\[ \Rightarrow A - B = 90^\circ \]
We can write this equation in angle form,
\[ \Rightarrow \angle A - \angle B = 90^\circ {\rm{ }}...{\rm{(ii)}}\]
By adding Eqs.(i) and (ii), we get
\[\angle 2A = 210^\circ \]
On simplification, we get
\[ \Rightarrow \angle A = \dfrac{{210^\circ }}{2} = 105^\circ \]
After putting the value of \[\angle A\] in Eq.(i). We get
\[\begin{array}{l}
105^\circ + \angle B = 120^\circ \\
 \Rightarrow \angle B = 120^\circ - 105^\circ = 15^\circ
\end{array}\]
This is the required solution.

So, the correct answer is “Option A”.

Note: Calculation plays an important role in these types of trigonometric problems.
Students should know the angle property that the sum of all internal angles of a triangle is always \[180^\circ \].
In this problem, while using formulas student can do mistake like \[\tan \left( {\dfrac{{A - B}}{2}} \right) = \dfrac{{a + b}}{{a - b}}\cot \left( {\dfrac{C}{2}} \right)\] instead of \[\tan \left( {\dfrac{{A - B}}{2}} \right) = \dfrac{{a - b}}{{a + b}}\cot \left( {\dfrac{C}{2}} \right)\]
Here, students must take while using trigonometric formulae.
There is an alternate method to solve this question.
We have sine rule,
\[\dfrac{{\sqrt 3 + 1}}{{\sin \left( {120 - x} \right)}} = \dfrac{{\sqrt 3 - 1}}{{\sin x}}\]
Now, we can rewrite this equation as,
\[ \Rightarrow \dfrac{{\sqrt 3 + 1}}{{\sqrt 3 - 1}} = \dfrac{{\sin \left( {120 - x} \right)}}{{\sin x}}\]
\[\begin{array}{l}
 \Rightarrow \tan x = 2 - \sqrt 3 \\
 \Rightarrow x = 15^\circ \\
\therefore \dfrac{{\angle A}}{{\angle B}} = \dfrac{7}{1}
\end{array}\]