Question

Which one of the following has point symmetry about the origin?
A.

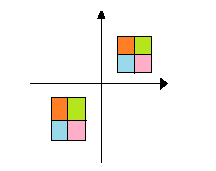
B

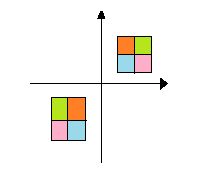
C

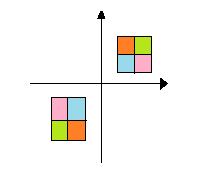
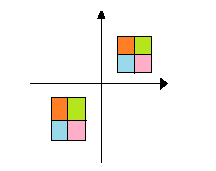
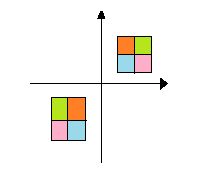
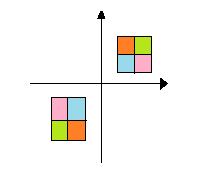
Answer 1

Hint: In point symmetry a figure when rotated has the same distance from the centre as before rotation but in opposite direction. It looks the same after rotation. Rotate the figures and see if the figures match after rotation of ${180^ \circ }$ .

Complete step-by-step answer:
Point symmetry is a symmetry in which every part of a figure has a matching part and the same distance from the centre point but in the opposite direction. It is also known as rotation symmetry of order $2$ .It means the shape looks the same after rotation of one turn or less than one turn.
In the figure A, when we rotate the figure ${180^ \circ }$ we get,

Here the arrows have the same distance from centre and in opposite directions but the position of colors has changed (on comparing with figure A) so it does not have a point symmetry about origin.
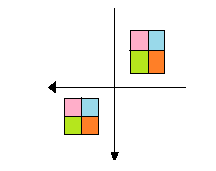
 When Figure B is rotated ${180^ \circ }$we get,

Here the arrows have the same distance from centre and in opposite direction but the position of colors has changed (on comparing with figure B) so it does not have a point symmetry about origin.
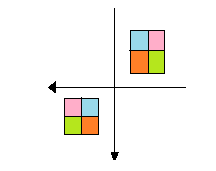
When figure C is rotated ${180^ \circ }$ we get,

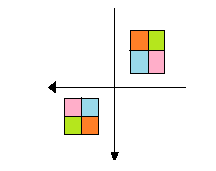
Here the arrows have the same distance from centre and in opposite directions. Also we see that the position of colors didn’t change (on comparing with figure C) so it does have a point symmetry about origin.
Hence the correct answer is C.
Note: Point symmetry is a form of rotational symmetry of order $2$.In this symmetry-
The center point is the point about which the image or figure is symmetrical.
The image or figure when turned upside down or rotated ${180^ \circ }$ has the same distance from the centre but in the opposite direction.
It is also called rotational symmetry of ${180^ \circ }$.