Question

Which of the following volume (V) – temperature (T) plots represents the behaviour of one mole of an ideal gas at one atmospheric pressure?

A)

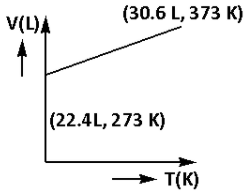
B)

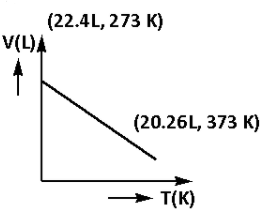
C)

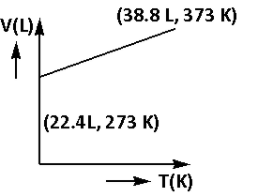
D)

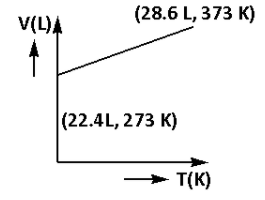
Answer 1

Hint: One mole of an ideal gas at standard temperature and pressure occupies 22.4 L of volume. Calculate the volume of ideal gas at 373 K using the ideal gas equation.

Complete answer:
One mole of an ideal gas at standard temperature and pressure occupies 22.4 L of volume.
This suggests that at the temperature 273 K and the pressure 1 atm one mole of an ideal gas occupies 22.4 L of volume.
Calculate the volume of the gas at 373 K using the ideal gas equation for one mole as follows:
PV = nRT
Where, P is the pressure of the ideal gas,
V is the volume of the ideal gas,
n is the number of moles of ideal gas,
R is the universal gas constant,
T is the temperature of the gas.
Rearrange the equation for the pressure as follows:
$V = \dfrac{{nRT}}{P}$
Substitute $1{\text{ mol}}$ for the number of moles, $0.082{\text{ L atm/K mol}}$ for the universal gas constant, $373{\text{ K}}$ for the temperature, $1{\text{ atm}}$ for the pressure. Thus,
$V = \dfrac{{1{\text{ mol}} \times 0.082{\text{ L atm/K mol}} \times 373{\text{ K}}}}{{1{\text{ atm}}}}$
V = 30.6 L
Thus, the volume of the gas at $373{\text{ K}}$ is $30.6{\text{ L}}$.
Thus, the plot that represents volume (V) – temperature (T) behaviour of one mole of an ideal gas at one atmospheric pressure is plot (A).

Thus, the correct option is (A).

Note: The pressure is kept constant and the volume and temperature are varied. Thus, Charles’s law can be applied in this case. Charles's law states that when the pressure of the gas is constant, the volume of the gas and the temperature of the gas are in direct proportion to each other. Thus, an alternative method to calculate the volume at $373{\text{ K}}$ is by using the equation of Charles’s law.