
Which of the following statements is true?
A) Intercept made by ax + by + c = 0 on the x – axis is $\dfrac{c}{a}$.
B) The line y = mx passes through the origin.
C) The line $y = \dfrac{1}{{\sqrt 3 }}x + 4$ makes an angle of ${60^ \circ }$ with the x – axis.
D) The line x = 7 is parallel to the x – axis.
Answer
577.2k+ views
Hint: We will check in all the given options by inspecting them one by one. We will put in the points in option 1 and 2 to see if they satisfy the equation or not. We will find the tangent of the angle and compare it with the slope in the third option. We will draw the line and see for ourselves in the last option.
Complete step-by-step answer:
Let us go through all the options one by one:
Option A: Intercept made by ax + by + c = 0 on the x – axis is $\dfrac{c}{a}$
If this statement is true, then the point where it makes the intercept at x – axis which is $\left( {\dfrac{c}{a},0} \right)$ must satisfy the equation of line. Therefore, let us put in $x = \dfrac{c}{a}$ and y = 0 in ax + by + c = 0.
$ \Rightarrow LHS = ax + by + c = a\left( {\dfrac{c}{a}} \right) + b(0) + c = 2c$
But RHS = 0. It is only possible if c = 0.
$\therefore $ option (A) is incorrect.
Option B: The line y = mx passes through the origin
If this statement is true, then the point $\left( {0,0} \right)$ must satisfy the equation of line. So, let us put in x = 0 and y = 0 in y = mx.
$ \Rightarrow 0 = m \times 0 = 0$ , which is always true.
$\therefore $ option (B) is correct.
Option C: The line $y = \dfrac{1}{{\sqrt 3 }}x + 4$ makes an angle of ${60^ \circ }$ with the x – axis
We know that slope is given by $\tan \theta $, where $\theta $ is the angle the line makes with the positive x – axis.
Since, the line given to us is given to make an angle of ${60^ \circ }$ with x – axis.
$ \Rightarrow Slope = m = \tan \left( {{{60}^ \circ }} \right) = \sqrt 3 $
But if we compare it to the given equation $y = \dfrac{1}{{\sqrt 3 }}x + 4$, the slope is the reciprocal.
$\therefore $ (C) is incorrect.
Option D: The line x = 7 is parallel to x – axis
Let us draw x = 7 in a coordinate axis.
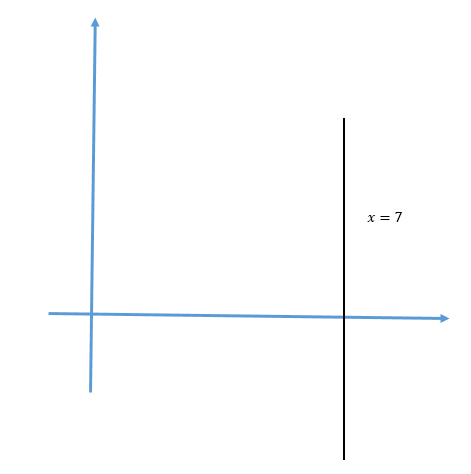
We clearly see that x = 7 is parallel to y – axis and perpendicular to x – axis.
$\therefore$(D) is incorrect.
Option B is the correct answer.
Note: The students must note that they need to know the basic details which are required in this solution. Like if a curve passes through a point, that point must satisfy the equation of the curve. Slope is given by the tangent of the angle, a line made with positive x – axis. And in option (4), you must draw the figure to get a clear picture.
The students must know that the general equation of a line is given by y = mx + c, where m is the slope of the line and c is the intercept it cuts and m is given by the tangent of the angle which line makes with the positive x – axis.
Complete step-by-step answer:
Let us go through all the options one by one:
Option A: Intercept made by ax + by + c = 0 on the x – axis is $\dfrac{c}{a}$
If this statement is true, then the point where it makes the intercept at x – axis which is $\left( {\dfrac{c}{a},0} \right)$ must satisfy the equation of line. Therefore, let us put in $x = \dfrac{c}{a}$ and y = 0 in ax + by + c = 0.
$ \Rightarrow LHS = ax + by + c = a\left( {\dfrac{c}{a}} \right) + b(0) + c = 2c$
But RHS = 0. It is only possible if c = 0.
$\therefore $ option (A) is incorrect.
Option B: The line y = mx passes through the origin
If this statement is true, then the point $\left( {0,0} \right)$ must satisfy the equation of line. So, let us put in x = 0 and y = 0 in y = mx.
$ \Rightarrow 0 = m \times 0 = 0$ , which is always true.
$\therefore $ option (B) is correct.
Option C: The line $y = \dfrac{1}{{\sqrt 3 }}x + 4$ makes an angle of ${60^ \circ }$ with the x – axis
We know that slope is given by $\tan \theta $, where $\theta $ is the angle the line makes with the positive x – axis.
Since, the line given to us is given to make an angle of ${60^ \circ }$ with x – axis.
$ \Rightarrow Slope = m = \tan \left( {{{60}^ \circ }} \right) = \sqrt 3 $
But if we compare it to the given equation $y = \dfrac{1}{{\sqrt 3 }}x + 4$, the slope is the reciprocal.
$\therefore $ (C) is incorrect.
Option D: The line x = 7 is parallel to x – axis
Let us draw x = 7 in a coordinate axis.
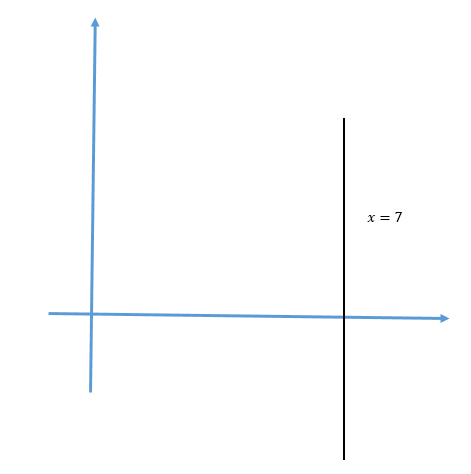
We clearly see that x = 7 is parallel to y – axis and perpendicular to x – axis.
$\therefore$(D) is incorrect.
Option B is the correct answer.
Note: The students must note that they need to know the basic details which are required in this solution. Like if a curve passes through a point, that point must satisfy the equation of the curve. Slope is given by the tangent of the angle, a line made with positive x – axis. And in option (4), you must draw the figure to get a clear picture.
The students must know that the general equation of a line is given by y = mx + c, where m is the slope of the line and c is the intercept it cuts and m is given by the tangent of the angle which line makes with the positive x – axis.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Which Country is Called "The Land of Festivals"?

What is Contraception List its four different methods class 10 biology CBSE




