Question

Which of the following pairs of triangles are congruent?
(Multiple answers from the options are correct)
A) $\Delta ABC$ and $\Delta DEF$ in which $BC = EF$ , \[AC = DF\] and $\angle C = \angle F$
B) $\Delta ABC$ and $\Delta DEF$ in which $AB = PQ$ , \[BC = QR\] and $\angle C = \angle R$
C) $\Delta ABC$ and $\Delta LMN$ in which $\angle A = \angle L = 90^\circ $ , \[AB = LM\] , $\angle C = 40^\circ $ and $\angle M = 50^\circ $
D) $\Delta ABC$ and $\Delta DEF$ in which $\angle B = \angle E = 50^\circ $ and \[AC = DF\]

Answer 1

Hint:
Firstly, by the information provided in the options, draw figures for each of the options.
Then, find the similarities between the two triangles.
If the similarity between them turns out to be true, then the triangles are congruent.
Thus, choose the correct options.

Complete step by step solution:
Here, we are asked to find congruence between the given triangles.
We will carry forward by checking every option individually.
Now, in option (A), two triangles $\Delta ABC$ and $\Delta DEF$ in which $BC = EF$ , \[AC = DF\] and $\angle C = \angle F$ .
We can draw their figures as per the information provided in the given option as

It is clear from the figure that, in the triangles $\Delta ABC$ and $\Delta DEF$ , they are congruent by SAS postulate.
Thus, $\Delta ABC \cong \Delta DEF$.
Similarly in option (B), two triangles $\Delta ABC$ and $\Delta DEF$ are given in which $AB = PQ$, \[BC = QR\] and $\angle C = \angle R$.
So, the figure for these triangles is

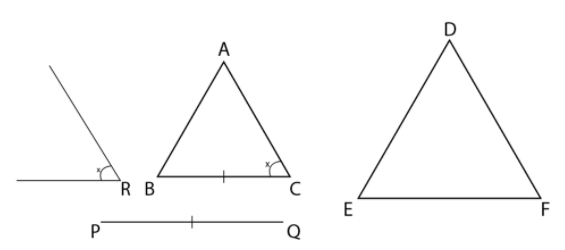
It is clear from the figure that the given triangles are not congruent as there is no similarity between them.
Thus, $\Delta ABC$ and $\Delta DEF$ are not congruent as there is no similarity between the two.
Also, in option (C) two triangles $\Delta ABC$ and $\Delta LMN$ are given in which $\angle A = \angle L = 90^\circ $ , \[AB = LM\] , $\angle C = 40^\circ $ and $\angle M = 50^\circ $ .
In $\Delta ABC$ , $\angle A = 90^\circ $ and $\angle C = 40^\circ $ and the sum of all angles of a triangle is $180^\circ $ .
 $\therefore \angle A + \angle B + \angle C = 180^\circ $
 $
  \therefore 90^\circ + \angle B + 40^\circ = 180^\circ \\
  \therefore \angle B = 180^\circ - 90^\circ - 40^\circ \\
  \therefore \angle B = 50^\circ \\
 $
And in $\Delta LMN$ , $\angle L = 90^\circ $ and $\angle M = 50^\circ $ and the sum of all angles of a triangle is $180^\circ $ .
 $\therefore \angle L + \angle N + \angle M = 180^\circ $
 $
  \therefore 90^\circ + \angle N + 50^\circ = 180^\circ \\
  \therefore \angle N = 180^\circ - 90^\circ - 50^\circ \\
  \therefore \angle N = 40^\circ \\
 $
So, the figure for these triangles is

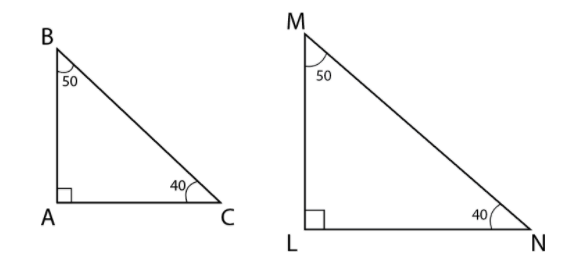
Thus, from the figure we can say that the triangles $\Delta ABC$ and $\Delta DEF$ are congruent to each other by AAA postulate.
So, $\Delta ABC \cong \Delta LMN$ .
In option (D) two triangles $\Delta ABC$ and $\Delta DEF$ are given in which $\angle B = \angle E = 50^\circ $ and \[AC = DF\] .
So, figure for these triangles is

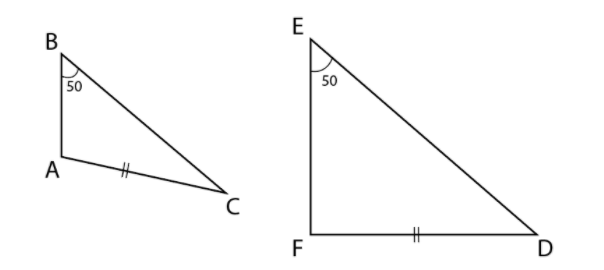
Thus, from the figure we can say that these triangles are not congruent. If there was given a third similarity between them, they would have been similar triangles.
So, $\Delta ABC$ and $\Delta DEF$ are not congruent.

Thus, options (A) and (C) are the correct answers.

Note:
The four ways to find the congruence between the two triangles are as follows.
(i) SSS postulate:
SSS stands for side, side, side. If three sides of one triangle are equal to three sides of another triangle, then the triangles are said to be congruent by SSS postulate.

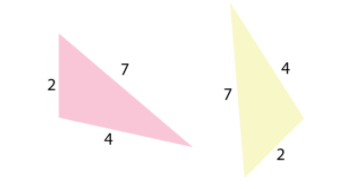
(ii) SAS postulate:
SAS stands for side, angle, side. If two sides and the included angle of a triangle are equal to the corresponding sides and angle of another triangle, then the triangles are said to be congruent by SAS postulate.

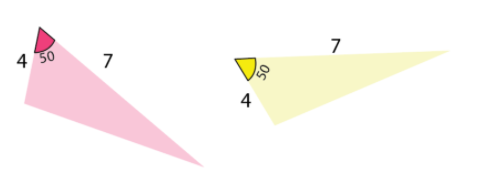
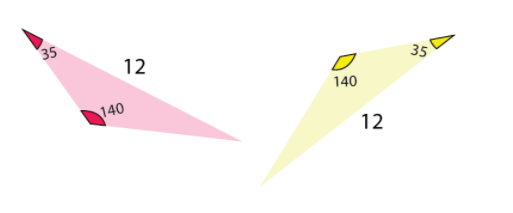
(iii) ASA postulate:
ASA stands for angle, side, angle. If two angles and the included side of a triangle are equal to the corresponding angles and side of another triangle, then the triangles are congruent by ASA postulate.

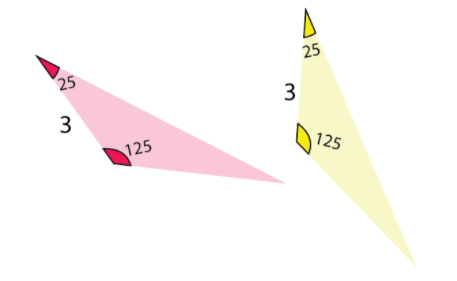
(iv) AAS postulate:
AAS stands for angle, angle, side. If two angles and the non-included side on a triangle are equal to the corresponding angles and side of another triangle, then the triangles are congruent by AAS postulate.