Question

Which of the following is not defined?
A. $\sin 90{}^\circ $
B. $\tan 0{}^\circ $
C. $\cot 90{}^\circ $
D. $\text{cosec }0{}^\circ $

Answer 1

Hint: We will first draw a right angle triangle and then we will observe the relation between sides and the given angle for the trigonometric ratios and then we will get the required value of the above question.

Complete step by step solution:
We have been asked to find which of the given is not defined i.e. $\sin 90{}^\circ $, $\tan 0{}^\circ $, $\cot 90{}^\circ $, $\text{cosec }0{}^\circ $
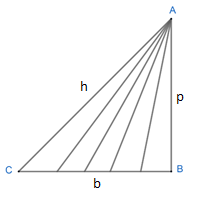
Let us consider a right angled triangle ABC, right angle at B.
Where AB = p = perpendicular, BC = b = base and AC = h = hypotenuse.
We will check the options one by one
A. $\sin 90{}^\circ $
We know sine of any angle is the ratio of perpendicular to hypotenuse.
In $\Delta ABC$
\[\sin C=\dfrac{p}{h}\]
If $\angle C$ tends to $90{}^\circ $, then h becomes equal to p.
$\Rightarrow \sin 90{}^\circ =\dfrac{p}{p}=1$

B. $\tan 0{}^\circ $
We know that tangent of any angle is the ratio of perpendicular to base.
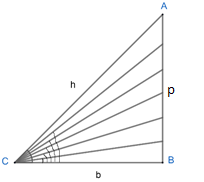
In \[\Delta ABC\]
\[\tan C=\dfrac{p}{b}\]
We can see from the diagram that if $\angle C$ tends to $0{}^\circ $, then p also tends to zero.
$\Rightarrow \tan 0{}^\circ =\dfrac{0}{b}=0$

C. $\cot 90{}^\circ $
We know that cotangent of any angle is the ratio of base to perpendicular.
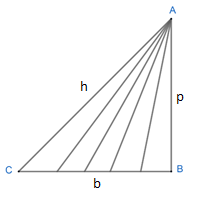
In \[\Delta ABC\]
\[\cot C=\dfrac{b}{p}\]
We can see that if $\angle C$ tends to $90{}^\circ $, then b also tends to zero.
\[\Rightarrow \cot 90{}^\circ =\dfrac{0}{p}=0\]

D. $\text{cosec }0{}^\circ $
We know that cosine of any angle is the ratio of hypotenuse to base.
In \[\Delta ABC\]
\[\text{cosec}C=\dfrac{h}{p}\]
If $\angle C$ tends to $0{}^\circ $, then p also tends to zero.
$\Rightarrow \text{cosec }0{}^\circ =\dfrac{h}{0}\to \infty $

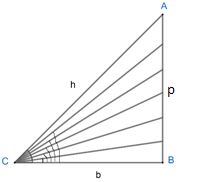
Hence, it is not defined.
Therefore, the correct option is D.

Note: We can also solve the given question with the help of trigonometric ratios table. Also, you must have to remember all the values for the trigonometric ratio given in the table, it will help you to solve these types of questions very quickly.