Question

Which of the following inequalities is equivalent to the absolute value inequality $|x - 3|\,\, \leqslant \,\,5$
A. $ - 2 \leqslant x \leqslant 8$
B. $ - 8 \leqslant x \leqslant 2$
C. $x \leqslant - 2\,\,or\,\,x \geqslant 8$
D. \[x \leqslant - 8\,\,or\,\,x \geqslant 2\]

Answer 1

Hint:
First, we will find the different inequalities when $x \geqslant 3$ and $x \leqslant 3$ since we know modulus gives a positive value for negative integer and positive value for positive integer we will find two inequalities and by merging these two inequalities we will find the required solution.

Complete step by step solution:
According to the question we need to find the inequalities equivalent to the absolute value inequality
 $|x - 3|\,\, \leqslant \,\,5$
Firstly, we need to make two cases
CASE – 1 $(x \geqslant 3)$
 $ \Rightarrow x - 3 \geqslant 0$
Here, Modulus returns the same value as it is positive
 $ \Rightarrow |x - 3\,|\,\, \leqslant \,\,5$
So, we have,

$ \Rightarrow x - 3\,\,\, \leqslant \,\,5$
On adding 3 to both sides we get,
 $ \Rightarrow x\,\,\, \leqslant \,\,5 + 3$
Hence, from case 1 we get
 $ \Rightarrow x\,\,\, \leqslant \,\,8$ …(1)
Now,
CASE – 2 $(x \leqslant 3)$
 $ \Rightarrow x - 3 \leqslant 0$
Hence, Modulus returns the negative of this value to provide the absolute value
 $ \Rightarrow |x - 3\,|\,\, \leqslant \,\,5$
So, we have,
 $ \Rightarrow - (x - 3\,)\,\, \leqslant \,\,5$
Multiplying -1 in both sides of the inequality we get
 $ \Rightarrow x - 3\,\,\, \geqslant \, - \,5$
Since multiplication of negative number changes the equality sign to its opposite
 $ \Rightarrow x\,\,\, \geqslant \, - \,5 + 3$
Hence, from case 2 we get
 $ \Rightarrow x\,\,\, \geqslant \, - \,2$ … (2)
Now merging equation (1) and (2) we get
 $ - 2 \leqslant x \leqslant 8$
Which is the same as Option A and equivalent to the absolute value inequality $|x - 3|\,\, \leqslant \,\,5$

So, A is the correct answer.

Note:
In the questions which contain mode functions, do remember that the equation containing mod function always has two solutions. This is because the mod function always has a single value of y at which two values of x are associated, this could be easily understood after observing the graph. That is

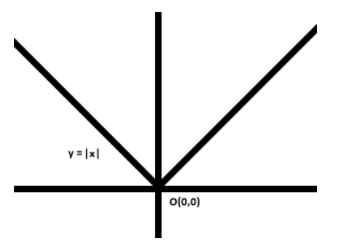
This is the graph of $|x|$.