Question

Which of the following conditions hold true for zeros of the quadratic polynomial ${{x}^{2}}+kx+k,k\ne 0$
[a] Cannot be both positive
[b] Cannot be both negative
[c] Are always equal
[d] Are always unequal.

Answer 1

Hint: Draw rough graphs of each of the following
[1] Both roots negative
[2] Both roots positive
[3] Roots are equal
[4] Roots are unequal.
Find the conditions of occurrence of each of these cases from the graph and hence find which of the options is correct and which is incorrect. Use the fact that the minima of a quadratic function $a{{x}^{2}}+bx+c,a>0$ occurs at $x=\dfrac{-b}{2a}$.

Complete step-by-step answer:
When both the roots are positive, the rough sketch of the graph of the quadratic function $f\left( x \right)=a{{x}^{2}}+bx+c,a>0$ is as follows

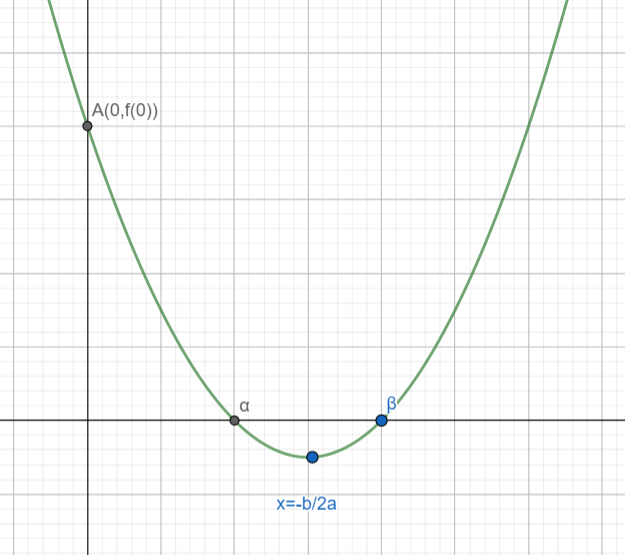
As is evident from the graph the condition that both the roots of the quadratic function $f\left( x \right)=a{{x}^{2}}+bx+c,a>0$ are positive is
[a] $f\left( 0 \right)>0$ (Because y-coordinate of C is positive)
[b] $\dfrac{-b}{2a}>0$( Because minima occurs in between the roots)
[c] $D={{b}^{2}}-4ac\ge 0$(Because roots are real)
Hence if the quadratic function $f\left( x \right)={{x}^{2}}+kx+k,k\ne 0$ has both roots positive, then
[a] $f\left( 0 \right)=0+k\left( 0 \right)+k=k>0$
[b] $\dfrac{-b}{2a}=\dfrac{-k}{2}>0$
We have $\dfrac{-k}{2}>0$
Multiplying both sides by 2, we get
$-k>0$
Adding k on both sides, we get
$0>k\Rightarrow k<0$
Hence, we have
$k>0$ and $k<0$, which is not possible.
Hence the quadratic function ${{x}^{2}}+kx+k,\ne 0$ cannot have both roots positive
Hence option [a] is correct
When both the roots are negative, the rough sketch of the graph of the quadratic function $f\left( x \right)=a{{x}^{2}}+bx+c,a>0$ is as follows

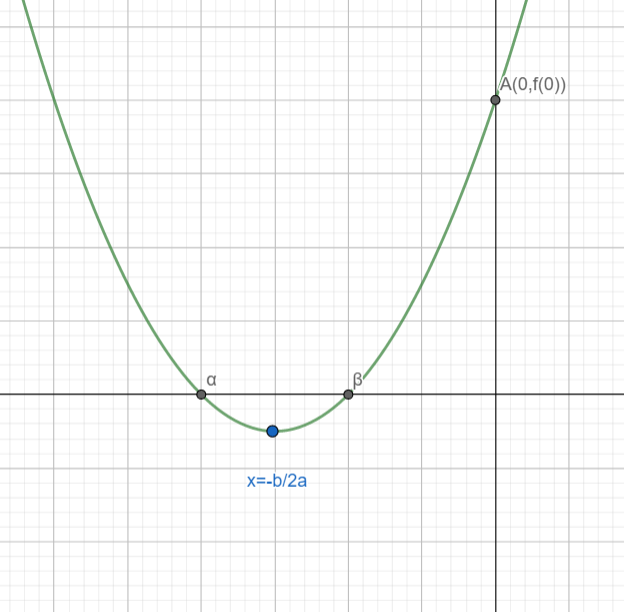
As is evident from the graph the condition that both the roots of the quadratic function $f\left( x \right)=a{{x}^{2}}+bx+c,a>0$ are negative is
[a] $f\left( 0 \right)>0$ (Because y-coordinate of C is positive)
[b] $\dfrac{-b}{2a}<0$( Because minima occurs in between the roots)
[c] $D={{b}^{2}}-4ac\ge 0$(Because roots are real)
Hence if the quadratic function $f\left( x \right)={{x}^{2}}+kx+k,k\ne 0$ has both roots negative, then
[a] $f\left( 0 \right)=0+k\left( 0 \right)+k=k>0$
[b] $\dfrac{-b}{2a}=\dfrac{-k}{2}<0$
We have $\dfrac{-k}{2}<0$
Multiplying both sides by 2, we get
$-k<0$
Adding k on both sides, we get
$k>0$
[c] ${{b}^{2}}-4ac={{k}^{2}}-4\left( 1 \right)k={{k}^{2}}-4k\ge 0$
Hence, we have
$k\left( k-4 \right)\ge 0$
By the method of intervals, we get
$k\in \left( -\infty ,0 \right]\bigcup \left[ 4,\infty \right)$
Taking all the conditions into consideration, we have
$k\in \left[ 4,\infty \right)$
Hence there exist values of k such that both the roots of the equation are negative.
Hence option [b] is incorrect.
When both roots of the quadratic function are equal, then the discriminant is 0.
Hence, for the quadratic function ${{x}^{2}}+kx+k,k\ne 0$ to have both roots equal, we have
${{b}^{2}}-4ac={{k}^{2}}-4k=0$
Hence, we have
$k\left( k-4 \right)=0$
Using zero product property, i.e. if ab = 0 then a = 0 or b=0, we get
k =0 or k=4
Since $k\ne 0$, we have k = 4.
Hence the roots of the quadratic equation are equal only when k = 4 and unequal otherwise.
Hence neither option [c] nor option [d] is correct.
Hence option [a] is the only correct answer.
Note: Alternatively, we can solve the question directly by finding the roots of the quadratic expression using the quadratic formula and verifying, which of the options is correct. This method, however, should be avoided as it usually leads to cumbersome calculations in which a student is likely to make a calculation mistake.