Question

Which of the following compounds will exhibit geometrical isomerism?
A. \[2 - phenyl - 1 - butene\]
B. \[1,1 - diphenyl - 1 - propane\]
C. \[1 - phenyl - 2 - butene\]
D. \[\;3 - phenyl - 1 - butene.\]

Answer 1

Hint: Geometrical isomerism is a type of stereoisomerism having the same molecular formula and same structure but differ in the relative arrangement of atoms. Geometric isomerism also known as Cis–Trans isomerism or configurational isomerism.

Complete step by step solution:
To identify geometrical isomerism it follow two conditions -
There are two necessary conditions for a compound to possess geometrical isomerism:
 (i) It must contain a carbon-carbon double bond in the molecule.
 (ii) Two unlike atoms or groups must be linked to each doubly bonded carbon atom.
Based on the group or atom attached to the carbon on each side with respect to double bond they are differentiate in two types - Cis isomer and –trans isomer.
If the two groups with the higher priorities are on the same side of the double bond, that is described as the (Cis)- isomer. If the two groups with the higher priorities are on opposite sides of the double bond, then this is the (Trans)-isomer.
As per given option – based on the conditions of geometrical isomerism-
 \[1 - phenyl - 2 - butene\] satisfies both the conditions.
It has 2 different groups on the left hand side and the right hand side. It has restricted rotation.
Thus this compound shows geometrical isomerism

The other structure in this option doesn’t follow the mentioned conditions in their structure. Its structure is given below –

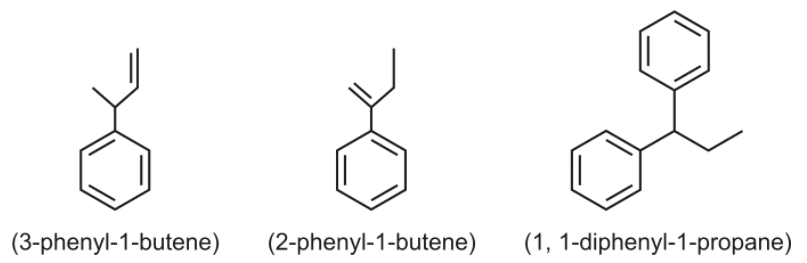
So, option (C) is correct

Note:
In geometrical isomerism, the double bond is planer so there is always \[{180^0}\] rotation during the conversion of Cis to Trans and Trans to Cis. Cis/Trans isomers also have similar chemical properties but different physical properties.