Question

What is the slope of the line \[3x+5y=15\]

Answer 1

Hint: This type of question is based on the concept of slope-intercept form of a line. The equation of a line in slope-intercept form is given by, \[y=mx+c\] where \[m\] is the slope and \[c\] is the y-intercept of the line. By rearranging the given equation of line in slope-intercept form we are able to find out the slope of the line.

Complete step by step solution:
Now, consider the equation of the given line which is \[3x+5y=15\]
Rearrange \[3x+5y=15\] in slope intercept form.
Move all the terms not containing y to the right side of the equation.
On Subtracting \[3x\] from both the sides, we get,
\[\Rightarrow 5y=15-3x\]
Now, dividing both sides by 5, we can write,
\[\Rightarrow \dfrac{5y}{y}=\dfrac{15}{5}-\dfrac{3}{5}x\]
\[\Rightarrow y=3-\left( \dfrac{3}{5} \right)x\]
We can rewrite the above equation as,
\[\Rightarrow y=-\left( \dfrac{3}{5} \right)x+3\]
This is nothing but the slope-intercept form of the given equation of line. So, we get,
\[\Rightarrow m=-\dfrac{3}{5}\]And \[c=3\]
The slope of the line is the value of \[m\] and the y-intercept is the value of \[c\].
Hence, Slope =\[m=-\dfrac{3}{5}\]and y-intercept = \[c=3\]
Therefore the slope of the equation of line \[3x+5y=15\] is \[-\dfrac{3}{5}\].

Note: Here, in case of finding slope of the equation of line \[3x+5y=15\] instead of using slope-intercept form students can use graphical method as follows,
First we to draw the graph of the equation of line \[3x+5y=15\] which is,

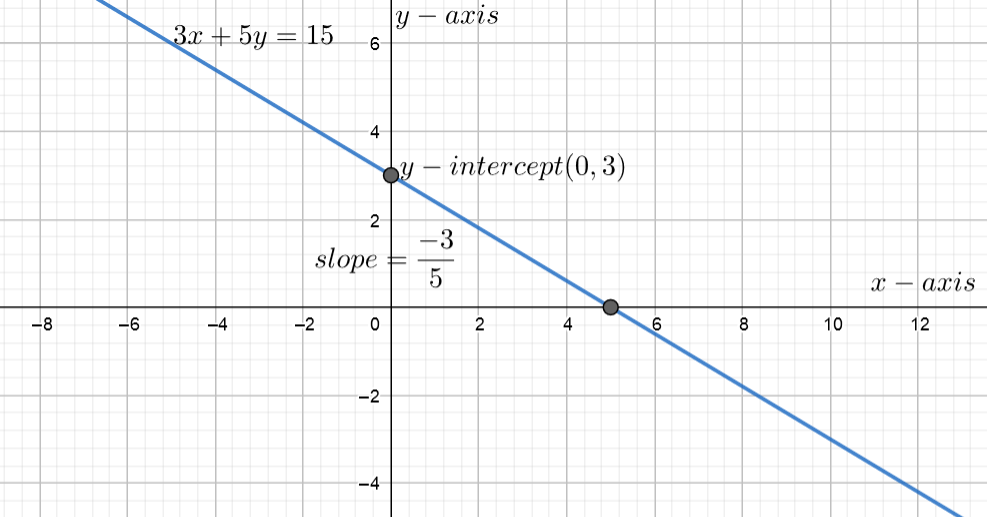
Here, \[A(0,3)\] and \[B(5,0)\] are two points on the given line.
So that, \[{{x}_{1}}=0,{{y}_{1}}=3,{{x}_{2}}=5\And {{y}_{2}}=0\]
Hence, slope of the corresponding line can be given by,
\[\Rightarrow m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\]
\[\Rightarrow m=\dfrac{0-3}{5-0}\]
\[\Rightarrow m=\dfrac{-3}{5}\]
\[\Rightarrow m=-\dfrac{3}{5}\]
Therefore the slope of the equation of line \[3x+5y=15\] is \[-\dfrac{3}{5}\].