Question

What is the shearing angle?

Answer 1

Hint: Shearing strain or shearing angle: It is defined as the ratio of angle \[\theta \] by which there is a relative displacement \[\Delta x\] between the opposite face of the object, because of tangential force acting on it as shown in the figure below.

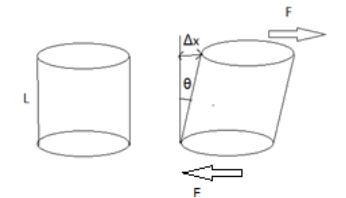
Shearing strain is generally caused because of two parallel forces acting in opposite directions.

Complete step by step solution:
When there is only change in the shape of an object due to tangential force the sharing angle for such deformation is expressed as
Shearing angle $ = \dfrac{\Delta x}{L} = \theta $
For such deformation, there is no change in the length \[L\] or volume of an object.
It is a dimensionless quantity.

Additional information:
Strain is defined as the ratio of change in length or volume or shape of an object because of an external force acting on a unit area.
Apart from shearing strain we also have longitudinal and volume stains and their definition are as follows
Longitudinal strain: it is defined as the change in length \[\Delta L\] of an object (cylindrical object) to its original length \[L\].
i.e., Longitudinal strain $ = \dfrac{\Delta L}{L}$
Volume strain: The strain produced by compressive stress is called volume strain and it is defined as the change in volume \[\Delta V\] of an object (cylindrical object) to its original volume \[V\] .
i.e., Volume strain $ = \dfrac{\Delta V}{V}$

Note:
Shearing angle is generally used to measure the deformation caused because of an external force acting on it tangentially.
And the exact formula for shearing strain is given as
$\dfrac{\Delta x}{L} = \tan \theta $
Here \[\tan \theta \] is considered as \[\theta \] since the shift in angle is considered very small for our simplicity.
And its unit is Radian or degree.