Question

What is the Pythagorean identity?

Answer 1

Hint: We first describe the Pythagorean identity with respect to the right-angle triangle. We use the formula of ${{\left( base \right)}^{2}}+{{\left( height \right)}^{2}}={{\left( hypotenuse \right)}^{2}}$. Putting the values, we get ${{a}^{2}}+{{b}^{2}}={{c}^{2}}$. Then we use the angles of the triangles to denote the sides and express it in the form of trigonometric ratios. We get ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$.

Complete step by step answer:
The Pythagorean identity is about the trigonometric identity that is used n case of right-angle triangle.
The Pythagorean trigonometric identity, also called simply the Pythagorean identity, is an identity expressing the Pythagorean theorem in terms of trigonometric functions. Along with the sum-of-angles formulae, it is one of the basic relations between the sine and cosine functions.
We express it for $\Delta ABC$ where $\angle B=\dfrac{\pi }{2}$.

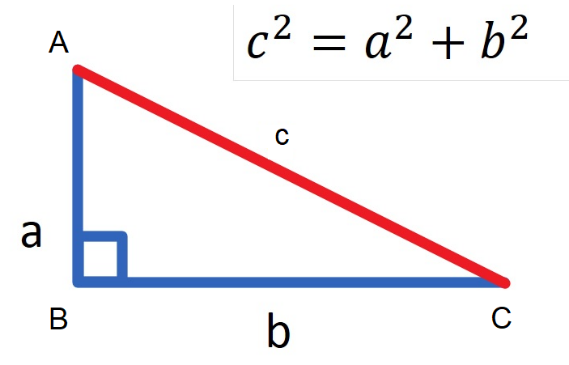
We have the expression for the triangle as ${{\left( base \right)}^{2}}+{{\left( height \right)}^{2}}={{\left( hypotenuse \right)}^{2}}$.
For $\Delta ABC$, $base=BC=b,height=AB=a,hypotenuse=AC=c$
Applying the rule, we get ${{\left( a \right)}^{2}}+{{\left( b \right)}^{2}}={{\left( c \right)}^{2}}$.
We can also express it with respect to the angle $\angle BCA$. Let $\angle BCA=\theta $.
The equation ${{\left( a \right)}^{2}}+{{\left( b \right)}^{2}}={{\left( c \right)}^{2}}$ can be simplified
$\begin{align}
  & {{a}^{2}}+{{b}^{2}}={{c}^{2}} \\
 & \Rightarrow {{\left( \dfrac{a}{c} \right)}^{2}}+{{\left( \dfrac{b}{c} \right)}^{2}}=1 \\
\end{align}$
With respect to the angle $\angle BCA=\theta $, we have $\dfrac{a}{c}=\sin \theta ,\dfrac{b}{c}=\cos \theta $.
Replacing the values, we get ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$.
There are many reformed versions of the formula ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$.
Dividing with ${{\cos }^{2}}\theta $, we got \[{{\tan }^{2}}\theta +1={{\sec }^{2}}\theta \].
Dividing with ${{\sin }^{2}}\theta $, we got \[{{\cot }^{2}}\theta +1={{\csc }^{2}}\theta \].

Note: The concept of Pythagorean identity is similar for both angles and sides. The representation of the triangle has to be for the right-angle triangle.