Question

What is the MOED of $H{e_2}$ molecule?

Answer 1

Hint: As we know that molecular orbital theory assumes that in molecules the atomic orbitals lose their identity and the electrons in molecules are present in new orbitals called molecular orbitals. Molecular orbitals energy diagrams show the relative energies of molecular orbitals.

Complete step by step answer:
The molecular orbital theory assumes that the atomic orbitals in molecules lose their identity and the electrons in these molecules are present in new orbitals which are commonly called molecular orbitals. When two atomic orbitals combine, formation of two molecular orbitals take place. The molecular orbitals formed by the overlapping of atomic orbitals is called bonding molecular orbital (BMO) and the molecular orbitals formed by the subtraction overlap of atomic orbitals is called anti-bonding molecular orbitals (ABMO).

Energy level diagrams for molecular orbitals can be drawn using the increasing order of energies which is given as:
$\sigma 1s < {\sigma ^*}1s < \sigma 2s < {\sigma ^*}2s < \sigma 2{p_z} < [\pi 2{p_x} = \pi 2{p_y}] < [{\pi ^*}2{p_x} = {\pi ^*}2{p_y}] < {\sigma ^*}2{p_z}$

As we know that Helium has an atomic number $2$. So the electronic configuration is $1{s^2}$and two atoms of helium are present so four electrons will be there in total which will accommodate the $\sigma 1s$ and ${\sigma ^*}1s$ molecular orbitals. Thus, we can draw the molecular orbital energy diagram as:

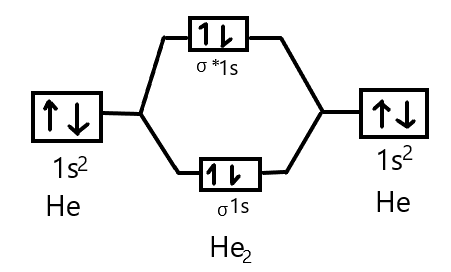
The stability of molecules can be determined by its bond order which is defined as the half the difference between the number of electrons in bonding molecular orbitals and the number of electrons in antibonding molecular orbitals. It is given as:
$Bond\;order = \dfrac{1}{2}[{N_b} - {N_a}]$
And we got from the diagram that Helium has two electrons in its bonding molecular orbital and two electrons in its anti-bonding molecular orbital. So its bond order will be:
$Bond\;order = \dfrac{1}{2}[2 - 2] = 0$
So, the bond comes out to be zero, therefore the $H{e_2}$ molecule is unstable and does not exist.

Note: Remember if the value of bond order is positive, it indicated that the molecule is stable and if the value of bond order is negative or zero then it suggests that the molecule is highly unstable and is not formed. The dissociation energy is directly proportional to the bond order of the molecule. Greater the bond order, greater will be the bond dissociation energy.