Question

What is the limit of a constant?

Answer 1

Hint: We know that for a limit to exist, the left hand limit and right hand limit must exist, and should be equal to one another and must also be equal to the value of function at that point. Using this definition, we can prove that the limit of a constant is nothing but itself.

Complete step by step answer:
We know that the limit of a function exists, only and only if the left hand limit (LHL) and the right hand limit (RHL) exists and are equal to one another. And, the value of the limit of that function is equal to the common value, LHL = RHL = f(x).
We need to find the limit of a constant. So, let us assume a function, $f\left( x \right)=c$, where c is a constant. We are assuming that we need to find the limit of this constant function at $x=a$,i.e., we need to find the value of $\displaystyle \lim_{x \to a}f\left( x \right)$.
Let us first plot the graph of y = c.

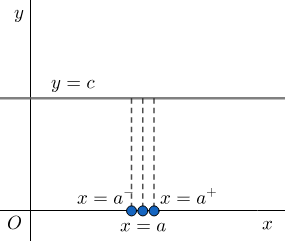
Let us calculate the left hand limit first.
LHL = $\displaystyle \lim_{x \to {{a}^{-}}}f\left( x \right)$
We can see that at $x={{a}^{-}}$, the value of $f\left( x \right)$ is c.
Hence, LHL = c …(i)
For right hand limit, we have
RHL = $\displaystyle \lim_{x \to {{a}^{+}}}f\left( x \right)$
We can see that at $x={{a}^{+}}$, the value of $f\left( x \right)$ is c.
Hence, RHL = c …(ii)
Also, the value of our function at a, i.e., \[f\left( a \right)=c\]…(iii)
Hence, by equation (i), (ii) and (iii), we can say that $\displaystyle \lim_{x \to a}f\left( x \right)=c$.
Or we can also write this as $\displaystyle \lim_{x \to a}\left( c \right)=c$.
Thus, we can now say that the limit of any constant is the same constant.
Hence, $\displaystyle \lim_{x \to a}\left( c \right)=c$.

Note: We must always remember that the limit of a constant value, is always that same value. We should not ignore any of the conditions that are required for the existence of limits at any point.