Question

What is the inverse cosine of 2?

Answer 1

Hint: We first find the principal value of x for which ${{\cos }^{-1}}\left( 2 \right)$. In that domain, equal value of the same ratio gives equal angles. We find the angle value for x. At the end we also find the general solution for the equation $\cos \left( x \right)=2$.

Complete step by step solution:
We find the value of ${{\cos }^{-1}}\left( 2 \right)$. We need to find x for which $\cos \left( x \right)=2$.
We know that in the principal domain or the periodic value of $-\dfrac{\pi }{2}\le x\le \dfrac{\pi }{2}$ for $\cos \left( x \right)$, if we get $\cos a=\cos b$ where $-\dfrac{\pi }{2}\le a,b\le \dfrac{\pi }{2}$ then $a=b$.
But the range for $\cos \left( x \right)$ is $-1\le \cos \left( x \right)\le 1$. So, it is not possible to find $x$ for which $\cos \left( x \right)=2$.
Now we prove that graphically.
We also can show the solutions (primary and general) of the equation $\cos \left( x \right)=2$ through the graph. We take $y=\cos \left( x \right)=2$. We got two equations $y=\cos \left( x \right)$ and $y=2$. We place them on the graph and find the solutions as their intersecting points.

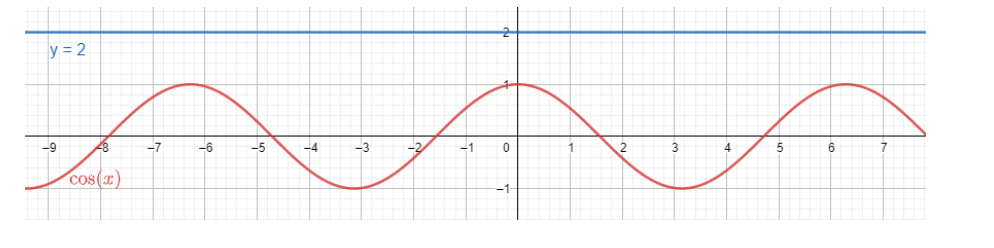
We can see that there is no intersecting point for the curves and the equation has no solution.


Note: Although for elementary knowledge the principal domain is enough to solve the problem. But if mentioned to find the general solution then the domain changes to $-\infty \le x\le \infty $. In that case we have to use the formula $x=n\pi \pm a$ for $\cos a=\cos b$ where $-\dfrac{\pi }{2}\le a\le \dfrac{\pi }{2}$.