Question

What is \[sec^{2}\left( \dfrac{\pi}{3} \right)\] ?

Answer 1

Hint: To understand the concept of \[\sec \theta \] we would have to consider a right-angle triangle, determine which side is to be considered as the base, perpendicular and the hypotenuse. The next step would be to assign the base angle as \[\theta \], determine the other sides and find the values of sin\[\theta \], cos\[\theta \], sec\[\theta \], tan\[\theta \] etc.,

Complete step-by-step answer:
Here we have been asked about sec\[\theta \]. To understand this, we need to consider a right-angle triangle, so let us draw a right-angle triangle.

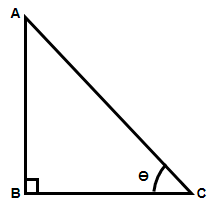
In the above figure we have considered a right angle triangle ABC right angle at B. Also, we have considered angle C equal to \[\theta \]. Now, let us see different elements of a right angle triangle such as its base, perpendicular and the hypotenuse.
Base and perpendicular of a right angle triangle is only defined when we define the angle \[\theta \]. The side which is opposite to the base angle \[\theta \] is the perpendicular side and the side which is opposite to the 90 degree angle is the hypotenuse. In this triangle, we have AB as the perpendicular and BC as the base.
Given, the value of \[\theta \] is \[\left( \dfrac{\pi }{3} \right)\] which is equal to \[{{60}^{\circ }}\]. So,
\[\begin{align}
  & \Rightarrow \operatorname{sec}\left( \dfrac{\pi }{3} \right)=\dfrac{1}{\operatorname{cos}\left( \dfrac{\pi }{3} \right)} \\
 & \Rightarrow \operatorname{sec}\left( \dfrac{\pi }{3} \right)=\dfrac{1}{\dfrac{1}{2}} \\
 & \Rightarrow \operatorname{sec}\left( \dfrac{\pi }{3} \right)=2 \\
\end{align}\]
Taking the square on both sides, we have
\[\begin{align}
  & \Rightarrow {{\operatorname{sec}}^{2}}\left( \dfrac{\pi }{3} \right)={{\left( 2 \right)}^{2}} \\
 & \Rightarrow {{\operatorname{sec}}^{2}}\left( \dfrac{\pi }{3} \right)=4 \\
\end{align}\]
\[\therefore \,\,{{\operatorname{sec}}^{2}}\left( \dfrac{\pi }{3} \right)=4\]

Note: Note that in a right-angle triangle the side which has the angle \[\theta \] is considered as the base of the triangle. If we will assume angle A as \[\theta \] then we will have AB as the base and BC as the perpendicular. The side which is opposite to the greatest angle is called the hypotenuse. Once we have determined which is the base, the hypotenuse and the base angle, it becomes simpler to find different trigonometric ratios.