Question

We define a lattice point as a point whose coordinates are integers, zero admitted. Then the number of lattice points on the boundary and inside the region bounded by the x-axis, y-axis, the line \[x = 4\], and the line \[y = 4\] is:
a. 24
b. 25
c. 34
d. 30
e. Not finite

Answer 1

Hint:
Initially, we try to find out the intersection points from all the equations given to us in the problem. The total number of integer points that lie on the equation will help us get the total number of lattice points.

Complete step by step solution:
We have here, 4 lines as the x axis, given as, \[y = 0\] , the y axis, given as, \[x = 0\] , and we also have the lines \[x = 4\] and \[y = 4\] .

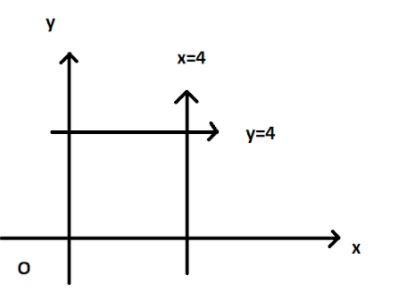
All the lattice points will lie on these lines, so solving for each,
\[y = 4\] , \[y = 0\] , \[x = 0\] , \[x = 4\]
The region contains, 5 lines, \[x = 0,1,2,3,4\] horizontally. All the lattice points will on these lines.
And again the region containing 5 lines, \[y = 0,1,2,3,4\] vertically. The lattice points will also be on these lines.
So, we have the integer values of x as 0, 1, 2, 3, 4 and y just the same.
But the value cannot be zero again so we will exclude the point \[(0,0)\] from our chosen lattice points.
So, we have,
The number lattice points would be,\[(5 \times 5) - 1 = 25 - 1 = 24\]

Hence, option (a) is correct.

Note:
A point lattice is a regularly spaced array of points.
In the plane, point lattices can be constructed having unit cells in the shape of a square, rectangle, hexagon etc. Unless otherwise specified, point lattices may be taken to refer to points in a square array, i.e., points with coordinates \[(m,n,.....)\] where m, n,… are integers. Such an array is often called a grid or a mesh.