Question

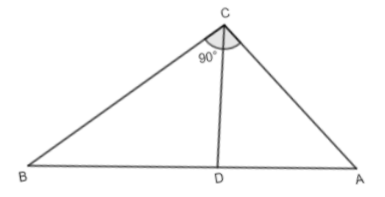
We are given an angle as $\angle ACB={{90}^{{}^\circ }}$ and $CD\bot AB$ , prove that $C{{D}^{2}}=AD\times BD$

Answer 1

Hint: To solve this question, firstly we will calculate the sum of two angles other than angle $\angle ADC={{90}^{{}^\circ }}$in triangle ADC. Then, we will calculate the sum of two angles other than $\angle ACB={{90}^{{}^\circ }}$in triangle ACB. Then, we will prove that $\angle ABC=\angle ACD$ and both triangles are similar. Hence, using similarity property inside of triangles we will prove that $C{{D}^{2}}=AD\times BD$.

Complete step-by-step solution
Now, in triangle ADC,
We know that the sum of the interior angles of a triangle is equal to ${{180}^{{}^\circ }}$.
So, $\angle ADC+\angle ACD+\angle DAC={{180}^{{}^\circ }}$
In question, it is given that $CD\bot AB$,
So, $\angle ADC={{90}^{{}^\circ }}$
Then, $\angle ACD+\angle DAC={{180}^{{}^\circ }}-{{90}^{{}^\circ }}$
$\angle ACD+\angle DAC={{90}^{{}^\circ }}$
Now, in triangle ACB,
$\angle ACB+\angle ABC+\angle DAC={{180}^{{}^\circ }}$, as sum of interior angles of triangle is equals to ${{180}^{{}^\circ }}$.
Now, as in question it is given that, $\angle ACB={{90}^{{}^\circ }}$
So, $\angle ABC+\angle DAC={{180}^{{}^\circ }}-{{90}^{{}^\circ }}$
On simplification, we get
$\angle ABC+\angle DAC={{90}^{{}^\circ }}$
Now, we got two conditions that $\angle ACD+\angle DAC={{90}^{{}^\circ }}$ and $\angle ABC+\angle DAC={{90}^{{}^\circ }}$.
So, using the above conditions, we can say that
$\angle ABC+\angle DAC=\angle ACD+\angle DAC$
Or, on simplification we get
$\angle ABC=\angle ACD$
Now, in triangle ADC and CBD we can easily see that
$\angle ABC=\angle ACD$
Also, $\angle CDB=\angle CDA$, as both are ${{90}^{{}^\circ }}$
So, we can say that both triangles are similar that is, $\vartriangle ADC\sim \vartriangle CDB$
So, if triangles are similar, then their sides are also similar.
Then using trigonometric ratio tangent in triangles $\vartriangle ADC\sim \vartriangle CDB$,we get
$\dfrac{BD}{CD}=\dfrac{CD}{AD}$ , as $\tan \theta= \dfrac{\text{Perpendicular}}{\text{Base}}$
Using cross multiplication, we get
$C{{D}^{2}}=BD\times AD$
Hence proved.

Note: To solve such questions, the best way is to prove triangles similar and for proving triangles similar, try to do some calculation such that you get two pair sides in the same ratios of both triangles or the angles are the same. Naming must be appropriate and try not to make any calculation errors and try to get more information or hint from the figure.