Question

How much water should be filled in a container 21cm in height so that it appears half-filled when viewed from the top of a container?
(Refractive index of water =$\dfrac{4}{3}$)
A. 8 cm
B. 10.5 cm
C. 12cm
D. 14 cm

Answer 1

Hint – We must know the formula of $(\dfrac{{{\text{real depth}}}}{{{\text{apparent depth}}}}) = \mu $ and the basic concept of refraction of light and basic calculations to find the level of water required to be filled for the given conditions to be possible.

Complete step-by-step solution -
When the light travels from rarer to the denser medium it bends towards normal to the surface of the medium and when it travels from denser to the rarer medium it bends away from the normal. This phenomena of bending of light is called refraction.
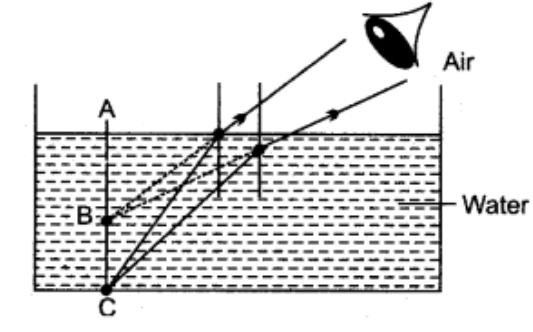
Let us say that the level of water is away from the top of the container AB by ‘x’ cm. The actual level of water would then be ‘21-x’ cm. Also, the apparent depth would be the same level ‘x’ cm.
The container will appear half filled when the appearance of point C will be in the place of B.
So, after using the formula we can say,
$(\dfrac{{{\text{real depth}}}}{{{\text{apparent depth}}}}) = \mu = \dfrac{4}{3}$
Hence we can say that,
$
  \dfrac{{21 - x}}{x} = \dfrac{4}{3} \\
  63 - 3x = 4x \\
  63 = 7x \\
  x = 9cm \\
$
Therefore, level of water required to be filled = (21-9) cm = 12cm
Hence, the correct option is C that is 12cm.

Note – We must be aware that the let quantity x is the level of water away from the top of the container and then apply the formula $(\dfrac{{{\text{real depth}}}}{{{\text{apparent depth}}}}) = \mu $ and then subtract the value of x from the height of the container in order to find the value of the level of water required. The situation said in this problem can be observed in daily life. As water is denser so the rays will bend towards normal and we will be seeing those parts from which the normal is striking.