Question

Water is flowing at the rate of 15 km per hour through a pipe of diameter 14 cm into a rectangular tank which is 50 m long and 44 m wide. Find the time in hours in which the level of water in the tank will rise by 21 cm. (Use $\pi =\dfrac{22}{7}$)

Answer 1

Hint: Let the length of the pipe be h. Find the volume of this pipe. Next, find the volume of the cuboidal tank. Equate these and find the value of h. This is the distance that water has to cover which is moving with the speed of 15 km/hr. Divide the distance by the speed to get the final answer.

Complete step-by-step answer:

In this question, we are given that water is flowing at the rate of 15 km per hour through a pipe of diameter 14 cm into a rectangular tank which is 50 m long and 44 m wide.

We need to find the time in hours in which the level of water in the tank will rise by 21 cm.

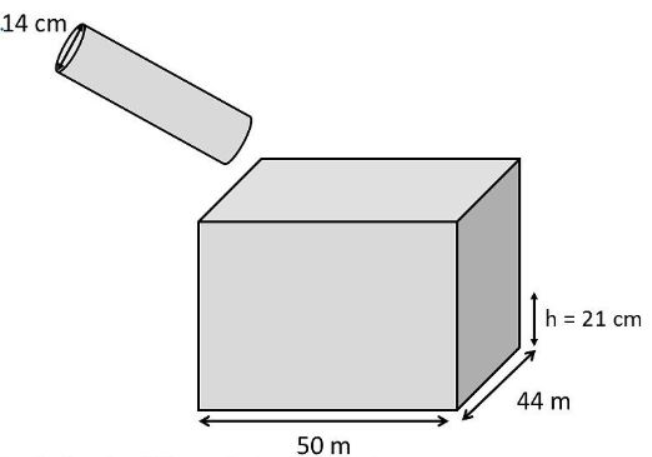
Let the length of the pipe for filling the whole tank be h m.

Pipe is in the form of a cylinder where height is h m and diameter is 14 cm.

We know that the radius is half of the diameter.

So, the radius of the pipe is 7 cm.

We know that the formula for volume of a cylinder is $\pi {{r}^{2}}h$.

Using this, the volume of the pipe is given by the following:

\[\pi {{r}^{2}}h=\pi {{\left( \dfrac{7}{100} \right)}^{2}}h=\dfrac{22}{7}\times
\dfrac{7}{100}\times \dfrac{7}{100}\times h\]

Now, the tank is in the form of a cuboid where l = 50 m, b = 44 m, h = 21 cm = 0.21 m

Volume of the tank = $lbh=50\times 44\times \dfrac{21}{100}=22\times 21$

The volume of the pipe = volume of the tank.

So, \[\dfrac{22}{7}\times \dfrac{7}{100}\times \dfrac{7}{100}\times h=22\times 21\]

$h=30000m=30km$

Water in the pipe flows at the rate of 15 km/hr .

Time taken by water to travel 30 km = $\dfrac{30km}{15km/hr}=2hrs$

So, the level of water in the tank will rise by 21 cm in 2 hours.

This is our final answer.

Note: Another way to solve this question can be the following. We find the volume of the cuboidal tank in the same way as done in the above solution. Calculate volume of cylinder by taking its height, h = 15 km which is the given speed in the question. Divide the volume of the tank by this to find the final answer. In this way, we are taking less time and effort to find the final answer.