Question

Water is filled to a height $H$ behind a dam of width $w$. The resultant force on dam is:
$\begin{align}
  & A)\rho gw{{H}^{2}} \\
 & B)\dfrac{1}{2}\rho gw{{H}^{2}} \\
 & C)2\rho gw{{H}^{2}} \\
 & D)4\rho gw{{H}^{2}} \\
\end{align}$

Answer 1

Hint: Pressure is defined as force per unit area. In other words, force is defined as the product of pressure and the area, on which the pressure is applied. A small strip of the length of the dam wall is considered at a particular distance from the surface of the vertical dam. Pressure on this small strip of the length of the dam wall and thus, the force on this small strip is determined. Force on the dam is nothing but the integral of this small force, acting on the small strip of the length of the dam wall.
Formula used:
$1){{P}_{x}}=\rho gx$
$2)dA=wdx$
$3)dF={{P}_{x}}\times dA$

Complete step-by-step solution
We are given that water is filled to a height $H$ behind a dam of width $w$. We are required to determine the resultant force on the dam.
Firstly, let us consider the figure given below. Clearly, $ABCD$ represents the vertical dam wall, filled with water filled up to a height of $H$, behind the dam, as shown. Also, the width of the dam is given by $w$.

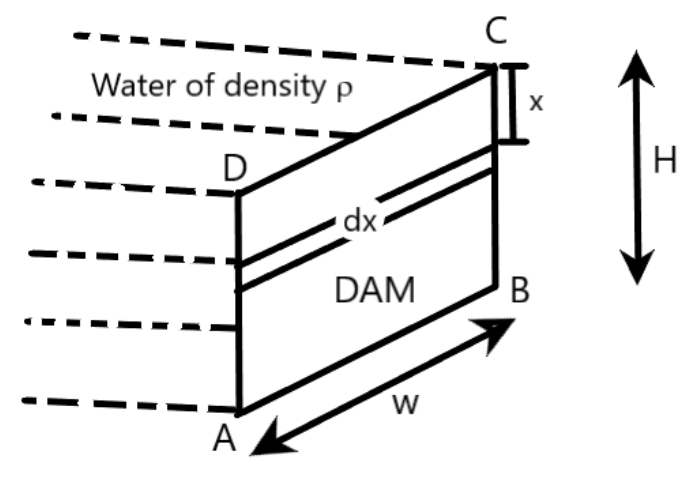
Now, let us consider a small strip of the length of the dam wall, at a distance $x$ from the top surface of the dam wall. The thickness of this small strip is assumed as $dx$. Clearly, water behind the dam exerts a horizontal pressure on this small strip of the dam wall. If ${{P}_{x}}$ represents the pressure on the small strip of dam wall of thickness $dx$ due to water behind it, then, ${{P}_{x}}$ is given by
${{P}_{x}}=\rho gx$
where
$\rho $ is the density of water behind the dam wall
$g$ is the acceleration due to gravity
$x$ is the distance of a small strip of dam wall from the top surface of the vertical dam wall
Let this be equation 1.
Also, if $dA$represents the area of a small strip of the dam wall, then, $dA$ is given by
$dA=wdx$
where
$w$ is the length of the small strip of the dam wall
$dx$ is the breadth or thickness of the small strip of the dam wall
Let this be equation 2.
Now, we know that the horizontal force on the small strip of the dam wall is equal to the product of pressure applied on this strip by the water behind the wall and the area of cross-section of the small strip of the dam wall. Clearly, if $dF$ represents the horizontal force exerted on the small strip of the length of the dam wall, then, $dF$ is given by
$dF={{P}_{x}}\times dA$
where
${{P}_{x}}$ is the pressure applied on the small strip of the length of dam wall by the water behind it
$dA$ is the area of cross-section of the small strip of the length of the dam wall
Let this be equation 3.
Substituting equation 1 and equation 2 in equation 3, we have
$dF={{P}_{x}}\times dA=\rho gx\times w dx=\rho gwx\;dx$
Let this be equation 4.
Now, taking the integral of equation 4 from zero to $H$, we have
$\int\limits_{0}^{H}{dF}=F=\int\limits_{0}^{H} \rho gwx dx =\rho gw\int\limits_{0}^{H} x dx =\rho gw\left( \dfrac{{{H}^{2}}}{2} \right)=\dfrac{1}{2}\rho gw{{H}^{2}}$
where
$F$ is the total horizontal force acting on the vertical dam wall due to the water behind it
$\rho $ is the density of water
$g$ is the acceleration due to gravity
$w$ is the width of the dam
$H$ is the height up to which water is filled behind the dam
Let this be equation 5.
Clearly, from equation 5, the resultant force acting on the dam wall is equal to $\dfrac{1}{2}\rho gw{{H}^{2}}$
Therefore, the correct answer is option $B$.

Note: Students need to adapt this method of taking small cross-sectional areas whenever they are dealing with problems involving volume, area, pressure, or force related to fluids. Determining the required parameter on these small cross-sectional areas, and then integrating them over the necessary values will provide appropriate results, as done in the above solution. Thus students need to be thorough with integral formulas too. The integral formula used in this solution is given as follows:
$\int\limits_{a}^{b}{{{x}^{2}}}dx=\dfrac{{{a}^{2}}}{2}-\dfrac{{{b}^{2}}}{2}$