Question

Water flows at the rate of 10m per minute through a cylindrical pipe having its diameter as 5mm. How much time will it take to fill a conical vessel whose diameter of the base is 40cm and depth is 24cm.

Answer 1

Hint: In this question, first of all, draw the diagram to visualize the question. Now, find the volume of the conical vessel by the volume of the water flowing through the pipe in 1 minute. Now, divide these values to find the time taken to fill the conical vessel.

Complete step-by-step solution -
We are given that the water flows at the rate of 10m per minute through a cylindrical pipe having its diameter as 5mm. We have to find the time it will take to fill a conical vessel whose diameter of the base is 40cm and depth is 24cm. Let us see the question diagrammatically.
 

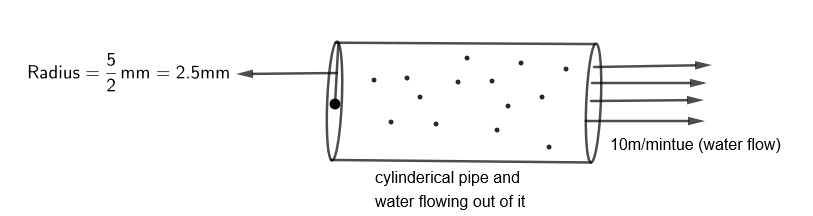
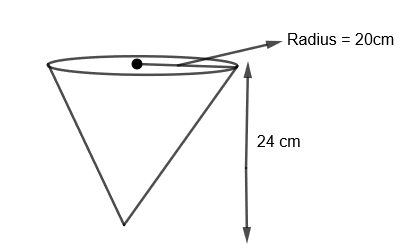
Here, we have to fill the conical vessel of the diameter 40cm and depth 24cm. So, first of all, we need to find the capacity of water that the conical vessel can hold. To find the capacity of the conical vessel, we have to calculate its volume.
We know that volume of the cone \[=\dfrac{1}{3}\pi {{r}^{2}}h\]
By substituting the value of \[r=\dfrac{40}{2}=20cm\] and h = 24cm, we get,
The volume of the conical vessel \[=\dfrac{1}{3}\pi {{\left( 20 \right)}^{2}}\times 24c{{m}^{3}}\]
\[=\dfrac{1}{3}\times \pi \times 400\times 24c{{m}^{3}}\]
\[=3200\pi \text{ }c{{m}^{3}}\]
Now, let us find the volume of water that flows through the cylindrical pipe in 1 minute. So, we get,
The volume of water that flows through a cylindrical pipe \[=\pi {{r}^{2}}\] [water flowing in 1 minute]
By substituting the value of \[r=\dfrac{5}{2}mm=2.5mm=\dfrac{2.5}{10}cm\] and water flowing in 1 minute = 10m = 1000 cm, we get,
The volume of water that flows through the cylindrical pipe in 1 minute \[=\pi {{\left( \dfrac{2.5}{10} \right)}^{2}}\times 1000\dfrac{\text{c}{{\text{m}}^{3}}}{\text{minute}}\]
So, we get the total time taken to fill the conical vessel
\[=\dfrac{\text{Volume of conical vessel}}{\text{Volume of water that flows through the pipe in 1 minute}}\]
\[=\dfrac{3200\pi \text{ c}{{\text{m}}^{3}}}{62.5\pi \text{ }\dfrac{\text{c}{{\text{m}}^{3}}}{\min }}\]
= 51.2 minutes.
Hence, we get the total time taken to fill the conical vessel as 51.2 minutes.

Note: In this question, students must take care that the diameters are given, So first convert it into the radius, and then only substitute in formulas. Also, take special care of the units. All the quantities must be converted into single units and basic conversions like 1m = 100 cm = 1000 mm should be there in mind. Also, in questions of mensuration, it is always better to draw the diagram of the given situation to visualize the question.