Question

What is \[{{\text{V}}_{{\text{rms}}}}\;\] of \[S{O_2}\;\]at \[300{\text{ }}K\]?
A.\[1.17{\text{m/s}}\]
B.$3.41{\text{m/s}}$
C.$341{\text{m/s}}$
D.None of these

Answer 1

Hint: To answer this question, recall the concept of root-mean-square speed of gas. Study the dependence of factors which affect this root mean square speed. Now use these factors to find the answer to this question.
 The formula used:
 ${{\text{v}}_{{\text{rms}}}} = \sqrt {\dfrac{{3{\text{RT}}}}{{\text{M}}}} $where ${{\text{v}}_{{\text{rms}}}}$= Root mean square speed, ${\text{R}}$ = Universal gas constant, ${\text{T}}$ = Temperature and ${\text{M}}$ is the Molar Mass of gas ---(i)

Complete step by step answer:
The root mean square speed t is the square root of the average velocity-squared of the molecules in a gas. You can see that it takes into account both molecular weight and temperature, these factors directly affect the kinetic energy of a gas.
From equation (i) we have the known values as Mass, \[{\text{M}} = 64{\text{g}} = 64 \times {10^{ - 3}}{\text{kg}}\], the universal gas constant, ${\text{R}}$=$8.31{\text{J/mol}}{\text{.K}}$and ${\text{T}}$=\[300{\text{ K}}\].
Substituting these known values with appropriate units into the equation we have,
\[{{\text{V}}_{{\text{rms}}}} = \sqrt {\dfrac{{3{\text{RT}}}}{{\text{M}}}} \]
\[ \Rightarrow {{\text{V}}_{{\text{rms}}}} = \sqrt {\dfrac{{3 \times 8.31 \times 300}}{{64 \times {{10}^{ - 3}}}}} = 3.41 \times {10^2}{\text{m/s}} = 341{\text{m/s}}\]

Hence, the correct option is option C.

Note:
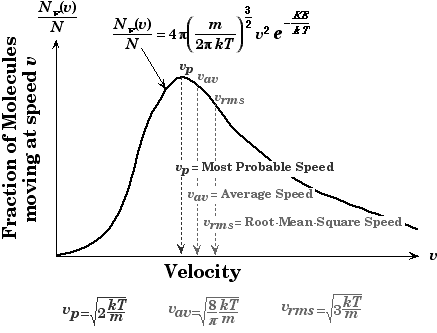
Make sure you remember that at conditions of high temperature and lower pressure, a real gas behaves like an ideal gas, because the potential energy due to intermolecular attractive forces becomes less significant compared with the particles’ kinetic energy, and the size of the molecules becomes less significant compared to the space between them. Along with different speeds, you should know the concept of the Maxwell-Boltzmann equation. The Maxwell-Boltzmann equation helps define the distribution of speeds for gas at various temperatures. From this distribution graph function, the most probable speed, the average speed, and the root-mean-square speed can be derived. The most probable speed is the speed most likely to be possessed by any molecule in the system.