Question

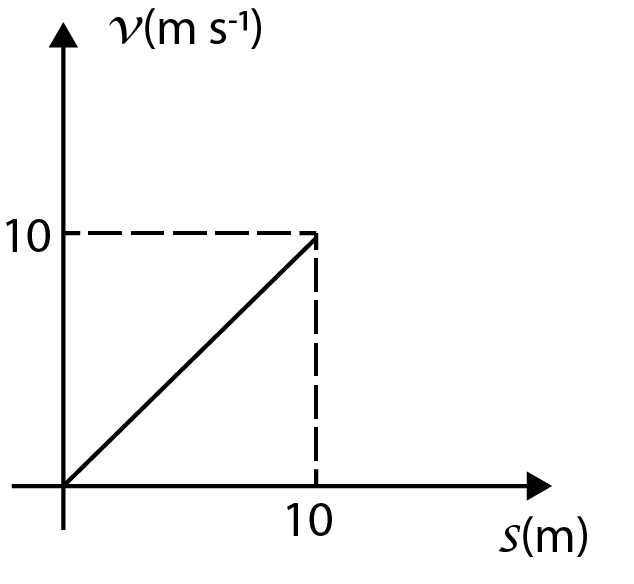
Velocity versus displacement graph of a particle moving in a straight line is shown in Fig. A.5. The corresponding acceleration versus velocity graph will be

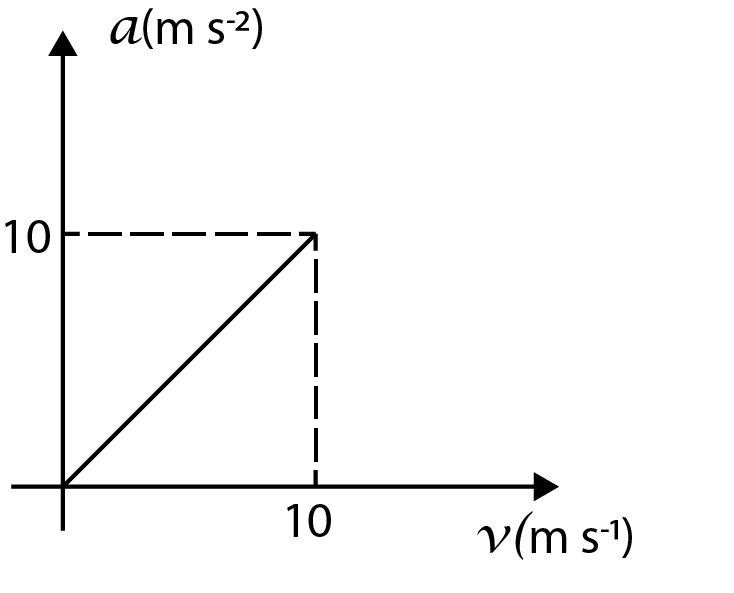
A.

B.

C.

D.

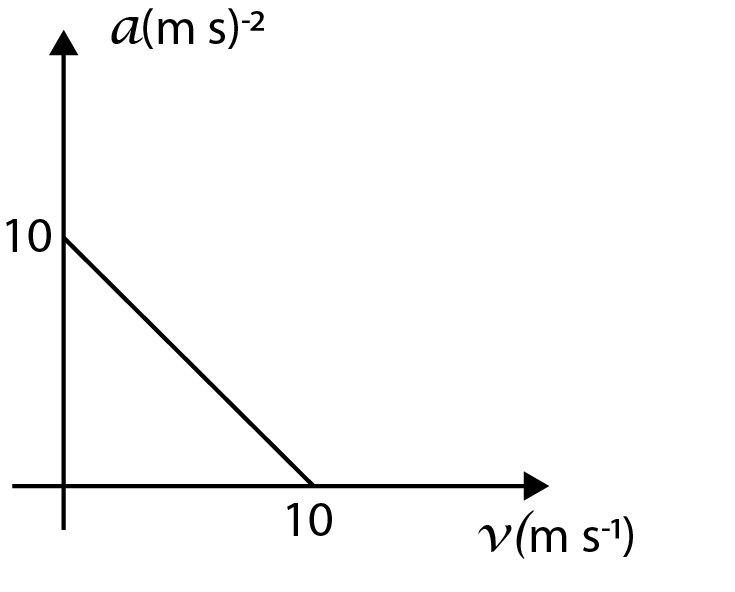
Answer 1

Hint: To solve the question, you first need to find slope of the curve given in the question, and represent the slope as $m = \dfrac{{dv}}{{dx}}$ since the quantity velocity is on the y-axis while the quantity displacement is on the x-axis of the graph. Then you need to represent acceleration in terms of velocity using the term $\dfrac{{dv}}{{dx}}$ and later substituting the value of the slope to find a direct relationship between velocity and acceleration.

Complete answer:
We will proceed with the solution exactly as explained in the hint section of the solution to the question.
As we can see in the given graph, the slope of the line can be given as:
$m = \dfrac{{dv}}{{dx}} = \dfrac{{{v_2} - {v_1}}}{{{x_2} - {x_1}}}$
If we substitute the value of coordinates of the two extreme points on the curve as $\left( {0,0} \right)$ and $\left( {10,10} \right)$ , we get the value of the slope of the curve as:
$\dfrac{{dv}}{{dx}} = \dfrac{{10 - 0}}{{10 - 0}} = 1$
Now, we can see that $\dfrac{{dv}}{{dx}} = 1$
Let us write acceleration in terms of differentials:
$a = \dfrac{{dv}}{{dt}}$
If we multiply and divide the right-hand side of the equation by $dx$ , we get:
$a = \dfrac{{dv}}{{dx}} \times \dfrac{{dx}}{{dt}}$
We already know that velocity is given as:
$v = \dfrac{{dx}}{{dt}}$
So, the equation of acceleration becomes:
$
  a = v\dfrac{{dv}}{{dx}} \\
   \Rightarrow \dfrac{a}{v} = \dfrac{{dv}}{{dx}} \\
 $
If we substitute the value of the term $\dfrac{{dv}}{{dx}}$ as found out above, we get:
$\dfrac{a}{v} = \dfrac{{dv}}{{dx}} = 1$
After transposing, we get:
$a = v$
The curve for this equation will be nothing but a straight-line curve on which the value of acceleration is exactly the same as the value of velocity.
If we check the options, the only option whose curve matches with the curve that we described above is option (A).

Hence, the correct option is option (A).

Note:
The main confusion can be at the point that which straight-line curve is the correct one between option (A) and option (D). To solve this, we can clearly see in the curve given in the question that the initial value of velocity is zero, hence, the correct option will be the one where the straight line starts at origin and not from a constant value on the y-axis.