Answer
Verified402.9k+ views
Hint: The formula for acceleration due to gravity, that is, ‘g’ is given by: $g=\dfrac{GM}{{{R}^{2}}}$. Here, we can see that the acceleration due to gravity is affected by three different entities. “G” is the universal gravitational constant which is a constant. “M” is the mass of the Earth and “R” is the radius of the Earth. We shall see what are the factors that change at the equator of the Earth, so that the value of ‘g’ gets minimized.
Complete step by step answer:
We know that, while solving problems or when talking in general, we assume the Earth to be a perfect sphere. Well, this assumption leads us to believe that ‘g’ is constant everywhere on Earth.
In reality, Earth is not a perfect sphere, but somewhat elliptical. This distortion on Earth causes the variation in gravitational acceleration at all places on Earth but the mass remains constant as it is independent of the shape. This could be understood as follows:
The Earth is bulged about its diameter, that is it is somewhat like the figure shown below:
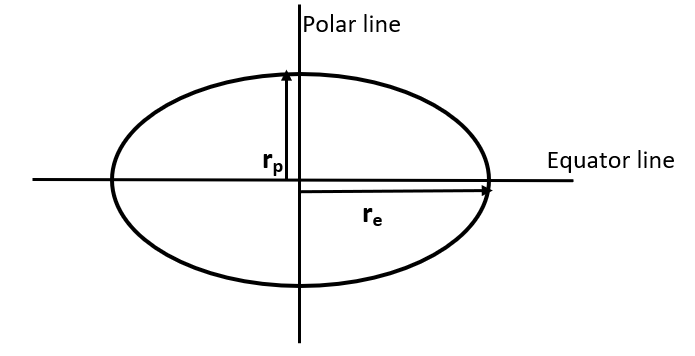
Here, we can see that the largest possible radius of Earth is equal to ‘${{r}_{e}}$’, that is, radius measured along the equator of Earth. This means that our expression for acceleration due to gravity is the least at the equator. Mathematically, this could be written as:
$\Rightarrow {{\left. \left( \dfrac{GM}{{{R}^{2}}} \right) \right|}_{\min }}=\left( \dfrac{GM}{{{r}_{e}}^{2}} \right)$
Hence, the value of ‘g’ minimum at the equator because the radius is maximum at the equator.
Note: Since the Earth is elliptical in shape, we see that its radius is minimum at the poles. Thus, we can say that poles are the places on Earth where maximum gravitational force is experienced whereas, all the places along the line of the equator experience minimum gravitational acceleration.
Complete step by step answer:
We know that, while solving problems or when talking in general, we assume the Earth to be a perfect sphere. Well, this assumption leads us to believe that ‘g’ is constant everywhere on Earth.
In reality, Earth is not a perfect sphere, but somewhat elliptical. This distortion on Earth causes the variation in gravitational acceleration at all places on Earth but the mass remains constant as it is independent of the shape. This could be understood as follows:
The Earth is bulged about its diameter, that is it is somewhat like the figure shown below:
Here, we can see that the largest possible radius of Earth is equal to ‘${{r}_{e}}$’, that is, radius measured along the equator of Earth. This means that our expression for acceleration due to gravity is the least at the equator. Mathematically, this could be written as:
$\Rightarrow {{\left. \left( \dfrac{GM}{{{R}^{2}}} \right) \right|}_{\min }}=\left( \dfrac{GM}{{{r}_{e}}^{2}} \right)$
Hence, the value of ‘g’ minimum at the equator because the radius is maximum at the equator.
Note: Since the Earth is elliptical in shape, we see that its radius is minimum at the poles. Thus, we can say that poles are the places on Earth where maximum gravitational force is experienced whereas, all the places along the line of the equator experience minimum gravitational acceleration.