Question

Using Theorem 1, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side.

Theorem 1 : If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.

Answer 1

Hint:In this question we will use the theorem 1 which states that : If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side. Using this theorem we have to prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side.

Complete step-by-step answer:
Let us assume a \[\vartriangle ABC\] in which $D{\text{ and E}}$are the mid points of sides $AB{\text{ and }}AC$ respectively.

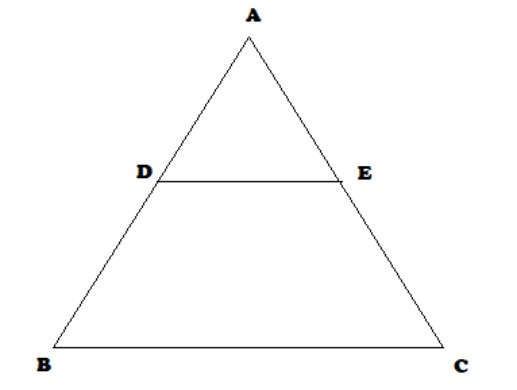
To prove : $DE||BC$ .
Proof :
Here , $D{\text{ and E}}$ are the mid points of $AB{\text{ and }}AC$
And we know that midpoint bisects a side into two equal parts .
So, $AD = DB{\text{ }}$.
$ \Rightarrow \dfrac{{AD}}{{DB}} = 1{\text{ }}$ ……(i)
Similarly we have , $AE = EC$
$ \Rightarrow \dfrac{{AE}}{{EC}} = 1$ …...(ii)
Equating equation (i) and (ii), we get
$ \Rightarrow \dfrac{{AD}}{{DB}} = \dfrac{{AE}}{{EC}}$ .
Thus ,the line DE divides the sides $AB{\text{ and }}AC$ of \[\vartriangle ABC\] in the same ratio, therefore by the converse of basic proportionality theorem ,we have
 $ \Rightarrow $ $DE||BC$

Note : In this type of problems we will use some theorems that have been already proved. First we have to make the figure related to the statement and then all the given details. Then we will write what we have to prove. After that we will use some basic theorems like here we have used the basic proportionality theorem which states that if line is drawn parallel to one side of triangle intersecting the other two sides, then it divides the two sides in the same ratio and then by using that theorem we have proved the statement.