Question

Using the vector method, find the incentre of the triangle whose vertices are P(0,4,0), Q (0,0,3) and R(0,4,3).

Answer 1

Hint: At first change the coordinates into vectors, then use $\overrightarrow{AB}=\overrightarrow{B}-\overrightarrow{A}$ to find $\overrightarrow{PQ},\overrightarrow{QR},\overrightarrow{RS}$ also find their absolute values. After getting use the formula of incentre which is,

$\overrightarrow{I}=\dfrac{\left| \overrightarrow{PQ} \right|.\overrightarrow{R}+\left| \overrightarrow{QR} \right|.\overrightarrow{P}+\left| \overrightarrow{RP} \right|.\overrightarrow{Q}}{\left| \overrightarrow{PQ} \right|+\left| \overrightarrow{QR} \right|+\left| \overrightarrow{RP} \right|}$

Complete step by step answer:
At first we will represent P in a vector form, so P will be equal to $\left( 0\widehat{i}+4\widehat{j}+0\widehat{k} \right)$ which can be written as $4\widehat{j}$ .
So, $\overrightarrow{P}=4\widehat{j}$.

Now we will represent Q in a vector form, so Q will be equal to $\left( 0\widehat{i}+0\widehat{j}+3\widehat{k} \right)$ which can be written as $3\widehat{k}$.
So, $\overrightarrow{Q}=3\widehat{k}$.

Now we will represent R in a vector form, so R will be equal to $\left( 0\widehat{i}+4\widehat{j}+3\widehat{k} \right)$ which can be written as $4\widehat{j}+3\widehat{k}.$

So, $\overrightarrow{R}=4\widehat{j}+3\widehat{k}$

Now we will find vectors $\overrightarrow{PQ},\overrightarrow{QR},\overrightarrow{RP}$ using formula, if $\overrightarrow{A}$ and $\overrightarrow{B}$ are vectors then $\overrightarrow{AB}=\overrightarrow{B}-\overrightarrow{A}$so,

$\overrightarrow{PQ}=\overrightarrow{Q}-\overrightarrow{P}=3\widehat{k}-4\widehat{j}$
$\overrightarrow{QR}=\overrightarrow{R}-\overrightarrow{Q}=\left( 4\widehat{j}+3\widehat{k} \right)-3\widehat{k}=4\widehat{j}$

$\overrightarrow{RP}=\overrightarrow{P}-\overrightarrow{R}=4\widehat{j}-\left( 4\widehat{j}+3\widehat{k} \right)=-3\widehat{k}$

Now we can find the absolute value of vector using formula, if $A=x\widehat{i}+y\widehat{j}+2\widehat{k}$, then $\left| A \right|=\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}$

Then,

$\left| \overrightarrow{PQ} \right|=\sqrt{{{\left( 0 \right)}^{2}}+{{\left( -4 \right)}^{2}}+{{\left( 3 \right)}^{2}}}=\sqrt{16+9}=5$

$\left| \overrightarrow{QR} \right|=\sqrt{{{\left( 0 \right)}^{2}}+{{\left( 4 \right)}^{2}}+{{\left( 0 \right)}^{2}}}=\sqrt{16}=4$

$\left| \overrightarrow{RP} \right|=\sqrt{{{\left( 0 \right)}^{2}}+{{\left( 0 \right)}^{2}}+{{\left( -3 \right)}^{2}}}=\sqrt{9}=3$

Now we will find the incentre by using the fact that the point is the intersection of three angle bisectors. We will use the formula,

$\overrightarrow{I}=\dfrac{\left| \overrightarrow{BC} \right|.\overrightarrow{A}+\left| \overrightarrow{CA} \right|.\overrightarrow{B}+\left| \overrightarrow{AB} \right|.\overrightarrow{C}}{\left| \overrightarrow{BC} \right|+\left| \overrightarrow{CA} \right|+\left| \overrightarrow{AB} \right|}$

Now we will put vectors $\overrightarrow{P,}\overrightarrow{Q},\overrightarrow{R}$ in the above formula so we can write it as,

$\overrightarrow{I}=\dfrac{\left| \overrightarrow{QR} \right|.\overrightarrow{P}+\left| \overrightarrow{RP} \right|.\overrightarrow{Q}+\left| \overrightarrow{PQ} \right|.\overrightarrow{R}}{\left| \overrightarrow{QR} \right|+\left| \overrightarrow{RP} \right|+\left| \overrightarrow{PQ} \right|}$

Now substituting the values we get,

$\overrightarrow{I}=\dfrac{4\left( 4\widehat{j} \right)+3\left( 3\widehat{k} \right)+5\left( 3\widehat{k}+4\widehat{j} \right)}{4+3+5}$

This can be simplified as,

\[\overrightarrow{I}=\dfrac{16\widehat{j}+9\widehat{k}+20\widehat{j}+15\widehat{k}}{12}\]

Hence,

$\overrightarrow{I}=\dfrac{36\widehat{j}+24\widehat{k}}{12}$

So,

$\overrightarrow{I}=3\widehat{j}+2\widehat{k}$

Hence the $\overrightarrow{I}$ can be represented in coordinates as (0, 3, 2).

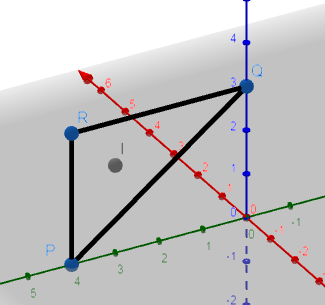
So, the coordinates of the triangle of the triangle is (0, 3, 2).

Note: Students should know the formula of how to represent the coordinates as a vector, finding the absolute value of a vector before doing these kinds of problems. They should also be careful about the calculation errors while dealing with vectors.
Students generally make an incentive formula. They may confuse it with the centroid of the triangle.