Question

Using the following data, draw a time-displacement graph for a moving object.

Time(S)	\[0\]	\[2\]	\[4\]	\[6\]	\[8\]	\[10\]	\[12\]	\[14\]	\[16\]
Displacement(m)	\[0\]	\[2\]	\[4\]	\[4\]	\[4\]	\[6\]	\[4\]	\[2\]	\[0\]

Use the graph to find average velocity for first \[4\] s, for next \[4\] s and for last \[6\] s?

Answer 1

Hint: We will draw time and displacement graph and then we will plot the above values in the graph to find the movement of the object.
Formula Used:
Average velocity of an object is total distance covered by the object divided by total time taken by the object.
\[{\text{Average velocity = }}\dfrac{{{\text{Total distance}}}}{{{\text{Total time}}}}\]

Complete step by step answer:
In the first \[4\] sec, the object took a time of total \[4\]sec and the object covered only \[4\]metre.
Similarly, for the next \[4\] sec the total time will be considered as \[4\]sec but it has the same displacement of \[4\]meter.
 But for the last \[6\]sec the total time taken will be \[6\]sec also but the displacement would be the slope of the graph moved from the two points.
So, we can draw the following graph to implement time and displacement:

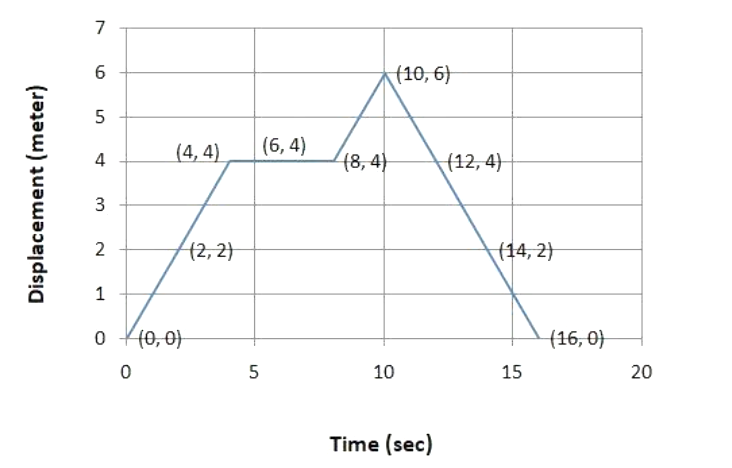
So, it is clearly seen in the above graph that for first \[0\]sec the object has no movement, but after another \[4\] sec the slope of the graph has been increased as the movement of the object has been increased accordingly.
But the object moved in the same horizontal zone as it moved the same distance from \[4\] sec to \[8\] sec, thus the slope of the graph became zero.
But, if we look closely in the graph, the slope of the graph is downgraded as the object moves from \[10\] sec to \[16\] sec, but there we can see the change in slope in the graph.
So, average velocity for the first \[4\] sec will be the total distance covered in the first \[4\] sec divided by total time taken.
So,
\[{\text{Velocit}}{{\text{y}}_{{\text{first 4sec}}}}{\text{ = }}\dfrac{{{\text{(4 - 0)}}}}{{{\text{(4 - 0)}}}}{\text{ = }}\dfrac{{\text{4}}}{{\text{4}}}{\text{ = 1}}\]\[m/\sec \]
For next \[4\]sec the velocity of the object will be the movement of the object in those \[4\] sec divided by the total time taken.
\[{\text{Velocit}}{{\text{y}}_{{\text{4s to 8s}}}}{\text{ = }}\dfrac{{{\text{(4 - 4)}}}}{{{\text{(8 - 4)}}}}{\text{ = }}\dfrac{{\text{0}}}{{\text{4}}}{\text{ = 0}}\]\[m/\sec \].
For the last \[6\]sec the movement of the object will be:
\[{\text{Velocit}}{{\text{y}}_{{\text{10s to 16s}}}}{\text{ = }}\dfrac{{{\text{(6 - 0)}}}}{{{\text{(16 - 10)}}}}{\text{ = }}\dfrac{{\text{6}}}{{\text{6}}}{\text{ = 1}}\]\[m/\sec \].
\[\therefore \]The required average velocities will be\[1m/\sec \],\[0m/\sec \] and \[1m/\sec \].

Note: From a particle’s movement in a velocity-time graph, its average velocity shall be count under the two different components:
Distance covered by the particle from a particular time slot and total time taken in that slot.