Question

Using integrations, find the area of the region common to the circle ${{x}^{2}}+{{y}^{2}}=16$ and the parabola ${{y}^{2}}=6x$ .

Answer 1

Hint: For solving this question, first we will plot the given curves on the same $x-y$ plane. Then, we will find the desired region whose area is asked in the question. After that, we will solve the given equations and find the coordinates of the intersection points. Then, we will take an elementary horizontal strip of width $dy$ and try to write its length in terms of the variable $y$ . Then, we will write the area of the elementary in terms of $y$ and $dy$ by multiplying its length and width. And finally, we will use the formula $\int{\sqrt{{{a}^{2}}-{{y}^{2}}}dy=\dfrac{y}{2}\sqrt{{{a}^{2}}-{{y}^{2}}}+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\left( \dfrac{y}{a} \right)}+c$ to integrate the area of the elementary strip with suitable limits to get the total area of the given region.

Complete step-by-step answer:
Given:
We have to find the area of the region common to the circle ${{x}^{2}}+{{y}^{2}}=16$ and the parabola ${{y}^{2}}=6x$ .
Now, before we proceed we should plot the curves ${{x}^{2}}+{{y}^{2}}=16$ and the ${{y}^{2}}=6x$ on the same $x-y$ plane. For more clarity, look at the figure given below:

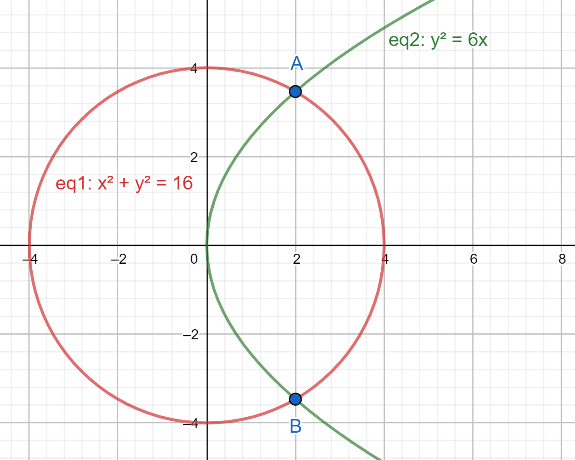
In the above figure, we have to find the area of the region bounded by the curves ${{x}^{2}}+{{y}^{2}}=16$ and the line ${{y}^{2}}=6x$ .
Now, from the above figure, we can say that for the coordinates of points A and B we should equate the equations ${{x}^{2}}+{{y}^{2}}=16$ and ${{y}^{2}}=6x$ . So, we put ${{y}^{2}}=6x$ in the equation ${{x}^{2}}+{{y}^{2}}=16$ . Then,
$\begin{align}
  & {{x}^{2}}+{{y}^{2}}=16 \\
 & \Rightarrow {{x}^{2}}+6x=16 \\
 & \Rightarrow {{x}^{2}}+6x-16=0 \\
\end{align}$
The above equation in quadratic in x so solving the above equation we get,
$\begin{align}
  & \Rightarrow {{x}^{2}}+8x-2x-16=0 \\
 & \Rightarrow x\left( x+8 \right)-2\left( x+8 \right)=0 \\
 & \Rightarrow \left( x-2 \right)\left( x+8 \right)=0 \\
\end{align}$
Equating $x-2$ to 0 we get,
$x-2=0$
Equating $x+8$ to 0 we get,
$x=-8$
Now, from the above result and the figure, we will neglect $x=-8$. We have neglected $x=-8$ because this point was not lying in the common region of the circle and the parabola and to get the coordinates of points A and B we should put $x=2$ in the equation ${{y}^{2}}=6x$ . Then,
$\begin{align}
  & {{y}^{2}}=6x \\
 & \Rightarrow {{y}^{2}}=6\times 2 \\
 & \Rightarrow {{y}^{2}}=12 \\
 & \Rightarrow y=\pm 2\sqrt{3} \\
\end{align}$
Now, from the above result and figure, we conclude that coordinates of points $A\equiv (2,2\sqrt{3})$ and $B\equiv (2,-2\sqrt{3})$ .
Now, we take an elementary horizontal strip at $y$ of width $dy$ . For more clarity, look at the figure given below:

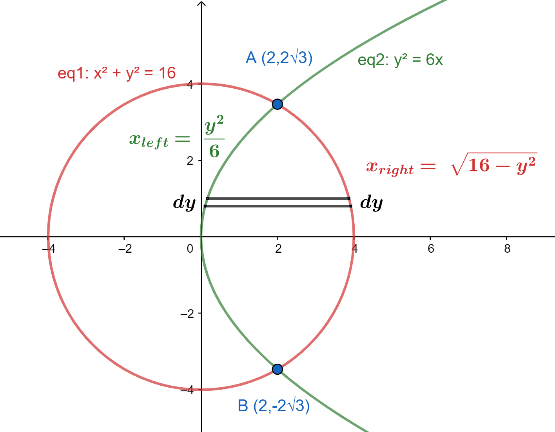
Now, here we should not take ${{x}_{right}}=-\sqrt{16-{{y}^{2}}}$ , because in the first and fourth quadrant $x>0$ .
Now, to find the length of the elementary strip, we should subtract the ${{x}_{right}}=\sqrt{16-{{y}^{2}}}$ and ${{x}_{left}}=\dfrac{{{y}^{2}}}{6}$ . Then,
length of the elementary strip $={{x}_{right}}-{{x}_{left}}=\sqrt{16-{{y}^{2}}}-\dfrac{{{y}^{2}}}{6}$ .
Now, as we know, the width of the elementary strip is $dy$ . So, the area of the elementary strip will be length multiplied by width. Then,
Area of the elementary strip $=dA=\left( \sqrt{16-{{y}^{2}}}-\dfrac{{{y}^{2}}}{6} \right)dy$ .
Now, to get the total area of the region, we should add the area of such elementary strips from $y=-2\sqrt{3}$ to $y=2\sqrt{3}$ so, to get the desired area we should integrate the expression $\left( \sqrt{16-{{y}^{2}}}-\dfrac{{{y}^{2}}}{6} \right)dy$ from $y=-2\sqrt{3}$ to $y=2\sqrt{3}$ . Then,
Area of the desired region \[=\int\limits_{-2\sqrt{3}}^{2\sqrt{3}}{\left( \sqrt{16-{{y}^{2}}}-\dfrac{{{y}^{2}}}{6} \right)dy}\] .
Now, we will use the formula $\int{{{y}^{n}}dy=\dfrac{{{y}^{n+1}}}{n+1}+c}$ and $\int{\sqrt{{{a}^{2}}-{{y}^{2}}}dy=\dfrac{y}{2}\sqrt{{{a}^{2}}-{{y}^{2}}}+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\left( \dfrac{y}{a} \right)}+c$ to integrate the above integral. Then,
\[\begin{align}
  & \int\limits_{-2\sqrt{3}}^{2\sqrt{3}}{\left( \sqrt{16-{{y}^{2}}}-\dfrac{{{y}^{2}}}{6} \right)dy} \\
 & \Rightarrow \left[ \dfrac{y}{2}\sqrt{16-{{y}^{2}}}+\dfrac{16}{2}{{\sin }^{-1}}\left( \dfrac{y}{4} \right)-\dfrac{{{y}^{3}}}{18} \right]_{-2\sqrt{3}}^{2\sqrt{3}} \\
\end{align}\]
Applying the upper and the lower limit in the above expression we get,
$
 \begin{align}
  & \left( \dfrac{2\sqrt{3}}{2}\times \sqrt{16-{{\left( 2\sqrt{3} \right)}^{2}}}+\dfrac{16}{2}{{\sin }^{-1}}\left( \dfrac{2\sqrt{3}}{4} \right)-\dfrac{{{\left( 2\sqrt{3} \right)}^{3}}}{18} \right)- \\
 & \left( \dfrac{-2\sqrt{3}}{2}\times \sqrt{16-{{\left( -2\sqrt{3} \right)}^{2}}}+\dfrac{16}{2}{{\sin }^{-1}}\left( \dfrac{-2\sqrt{3}}{4} \right)-\dfrac{{{\left( -2\sqrt{3} \right)}^{3}}}{18} \right) \\
\end{align}
$
\[\begin{align}
 & \Rightarrow \left[ \left( \sqrt{3}\times \sqrt{16-12}+8{{\sin }^{-1}}\left( \dfrac{\sqrt{3}}{2} \right)-\dfrac{24\sqrt{3}}{18} \right)-\left( -\sqrt{3}\times \sqrt{16-12}+8{{\sin }^{-1}}\left( -\dfrac{\sqrt{3}}{2} \right)+\dfrac{24\sqrt{3}}{18} \right) \right] \\
\end{align}\]
\[\begin{align}
  & \Rightarrow \left[ \left( \sqrt{3}\times \sqrt{4}+8{{\sin }^{-1}}\left( \dfrac{\sqrt{3}}{2} \right)-\dfrac{4}{\sqrt{3}} \right)-\left( -\sqrt{3}\times \sqrt{4}+8{{\sin }^{-1}}\left( -\dfrac{\sqrt{3}}{2} \right)+\dfrac{4}{\sqrt{3}} \right) \right] \\
 & \Rightarrow \left[ 2\sqrt{3}+8{{\sin }^{-1}}\left( \dfrac{\sqrt{3}}{2} \right)-\dfrac{4}{\sqrt{3}}+2\sqrt{3}-8{{\sin }^{-1}}\left( -\dfrac{\sqrt{3}}{2} \right)-\dfrac{4}{\sqrt{3}} \right] \\
 & \Rightarrow \left[ 4\sqrt{3}-\dfrac{8}{\sqrt{3}}+8{{\sin }^{-1}}\left( \dfrac{\sqrt{3}}{2} \right)-8{{\sin }^{-1}}\left( -\dfrac{\sqrt{3}}{2} \right) \right] \\
 & \Rightarrow \dfrac{4}{\sqrt{3}}+8{{\sin }^{-1}}\left( \dfrac{\sqrt{3}}{2} \right)-8{{\sin }^{-1}}\left( -\dfrac{\sqrt{3}}{2} \right) \\
\end{align}\]
Now, we will put ${{\sin }^{-1}}\left( \dfrac{\sqrt{3}}{2} \right)=\dfrac{\pi }{3}$ and ${{\sin }^{-1}}\left( -\dfrac{\sqrt{3}}{2} \right)=-\dfrac{\pi }{3}$ in the above. Then,
\[\begin{align}
  & \dfrac{4}{\sqrt{3}}+8{{\sin }^{-1}}\left( \dfrac{\sqrt{3}}{2} \right)-8{{\sin }^{-1}}\left( -\dfrac{\sqrt{3}}{2} \right) \\
 & \Rightarrow \dfrac{4}{\sqrt{3}}+8\times \dfrac{\pi }{3}-8\times \dfrac{-\pi }{3} \\
 & \Rightarrow \dfrac{4}{\sqrt{3}}+\dfrac{16\pi }{3} \\
\end{align}\]
Thus, the area of region common to the circle ${{x}^{2}}+{{y}^{2}}=16$ and the parabola ${{y}^{2}}=6x$ will be equal to $\dfrac{4}{\sqrt{3}}+\dfrac{16\pi }{3}\text{ sq}\text{.units}$ .

Note: Here, the student should first plot the given curves carefully and then find the desired region whose area is asked in the question and proceed in a stepwise manner. Then, we should be careful while writing the dimensions of the elementary strip and for that, we should take help from the plot of the given curves. Then, we should apply formulas like $\int{\sqrt{{{a}^{2}}-{{y}^{2}}}dy=\dfrac{y}{2}\sqrt{{{a}^{2}}-{{y}^{2}}}+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\left( \dfrac{y}{a} \right)}$ correctly. Moreover, for easy calculation, we could have written the area to be \[2\int\limits_{0}^{2\sqrt{3}}{\left( \sqrt{16-{{y}^{2}}}-\dfrac{{{y}^{2}}}{6} \right)dy}\] and solved further.