Question

Using integration, prove that the curves \[{y^2} = 4x\] and \[{x^2} = 4y\] divide the area of the square bounded by \[x = 0,x = 4,y = 0{\text{ and }}y = 4\] into 3 equal parts

Answer 1

Hint: Draw the \[{y^2} = 4x\],\[{x^2} = 4x\] graph and the square bounded by the $4$ lines to get a visual image for reference. You will realise that the two curves divide the square into $3$ regions. You need to prove that each of these regions is\[\dfrac{1}{3}{\text{rd}}\] of the area of the square. Integrate the area enclosed the\[{x^2} = 4y\]curve against the $x$-axis and the area enclosed by the \[{y^2} = 4x\]curve against the $y$-axis separately. Also calculate the area of the square.
Given: We are given the curve \[{y^2} = 4x\] and curve \[{x^2} = 4y\]
And the equations \[x = 0\],\[x = 4\],\[y = 0\]and \[y = 4\]that intersect to form a square.

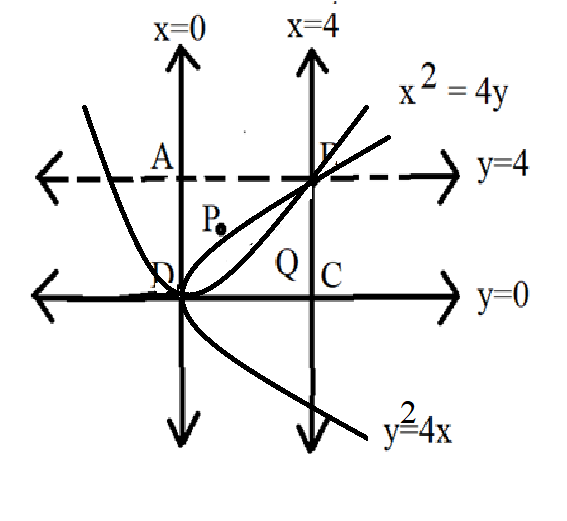
Complete step by step answer:
To prove that the area of the square is divided into $3$ parts by the curves.
That is, to prove that
\[
  {\text{ar DABP = ar DPBQ = ar DQBC = }}\dfrac{1}{3}{\text{arABCD}} \\
  {\text{ar ABCD = 4}} \times 4 = 16 \\
 \]
\[\therefore \dfrac{1}{3}{\text{ar ABCD = }}\dfrac{{16}}{3} = 5.33\;\;\;\;\;\; \ldots \left( i \right)\]
\[ar{\text{ DABP}}\] is the area enclosed by the curve \[{x^2} = 4y\] on the $x$-axis starting from \[x = 0\]to \[x = 4\].
Similarly, \[ar{\text{ DQBC}}\] is the area enclosed by the curve \[{y^2} = 4x\] on the $y$-axis starting from \[y = 0\] and \[y = 4\].
To calculate \[{\text{ar DQBC}}\],
\[{\text{ar DQBC = }}_0^4\smallint ydx\] [because area in on x-axis is]
\[
  {x^2} = 4y \\
   \Rightarrow y = \dfrac{{{x^2}}}{4} \\
  \therefore {\text{ar DQBC = }}_0^4\smallint \dfrac{{{x^2}}}{4}dx \\
   = \dfrac{1}{4}\left[ {\dfrac{{{x^3}}}{3}} \right]_0^4 \\
 \]
\[ = \dfrac{1}{{12}}\left( {{4^3}} \right) = \dfrac{{16}}{3}\;\;\;\;\;\;\; \ldots \left( {ii} \right)\]
From $\left( i \right)$ and $\left( {ii} \right)$ we get
\[{\text{ar DQBC = }}\dfrac{1}{3}{\text{ar ABCD}}\]
To calculate \[{\text{ar DABP}}\],
\[
  {\text{ar DABP = }}_0^4\smallint x{\text{dy}} \\
  {{\text{y}}^2} = 4x \\
   \Rightarrow x = \dfrac{{{y^2}}}{4} \\
  \therefore {\text{ar DABP = }}_0^4\smallint {\text{dy}} \\
  {\text{ = }}\dfrac{1}{4}\left[ {\dfrac{{{y^3}}}{3}} \right]_0^4 \\
 \]
\[ = \dfrac{1}{{12}}\left( {{4^3}} \right) = \dfrac{{16}}{3}\;\;\;\;\;\; \ldots \left( {iii} \right)\]
From $\left( i \right)$ and $\left( {iii} \right)$ we get,
\[{\text{ar DABP = }}\dfrac{1}{3}{\text{ar ABCD}}\]
\[{\text{ar DQBC + ar DABP + ar DPBQ = ar ABCD}}\] [from $\left( i \right)$]
\[ \Rightarrow \dfrac{1}{3}{\text{ar ABCD + }}\dfrac{1}{3}{\text{ar ABCD + ar DPBQ = ar ABCD}}\]
\[ \Rightarrow {\text{ar DPBQ = }}\dfrac{1}{3}{\text{ar ABCD}}\;\;\;\;\;\;\;\; \ldots \left( {iv} \right)\]
From$\left( {ii} \right)$ , $\left( {iii} \right)$ and $\left( {iv} \right)$ we get
\[{\text{ar DABP = ar DPBQ = ar DQBC = }}\dfrac{1}{3}{\text{ABCD}}\].

Note:
You can calculate \[{\text{ar DPBQ}}\]by integrating the region \[{\text{DPBC }}\]and subtracting\[{\text{ar DQBC}}\] from it. However, it is evident from the diagram that the curves \[{x^2} = 4y\] and \[{y^2} = 4x\] divide the square into $3$ regions. So, it is sufficient to prove that \[{\text{ar DABP = ar DQBC = }}\dfrac{1}{3}{\text{ABCD}}\] as it follows trivially that \[{\text{ar DPBQ}}\]must be \[{\text{ar ABCD - ar DABP = ar DQBC = }}\dfrac{1}{3}{\text{ar ABCD}}\]. The best way to solve coordinate geometry questions is to make a diagram and visualise areas from it.