Question

Using graph paper and taking 1 cm = 1 unit along both x-axis and y-axis
(i) Plot the point A (– 4, 4) and B (2, 2).
(ii) Reflect A and B in the origin to get the images A’ and B’ respectively.
(iii) Write down the coordinates of A’ and B’
(iv) Give the geometrical name for the figure ABA’B’.
(v) Draw and name its line of symmetry

Answer 1

Hint: At first plot point A in the second coordinate and point B in the first coordinate. Now, to get the images A’ and B’ reflect the points A and B respectively in the y-axis and after that in the x-axis. Note the coordinates while going through the process. Check the properties of the quadrilateral formed to get its name. Finally, check the lines which will cut the obtained quadrilateral into two equal halves to obtain the line of symmetry.

Complete step by step answer:
Here, we have been provided with a graph paper in which we have to take 1 cm = 1 unit along both the x and y-axis. We have been provided with five questions. Let us check them one by one.
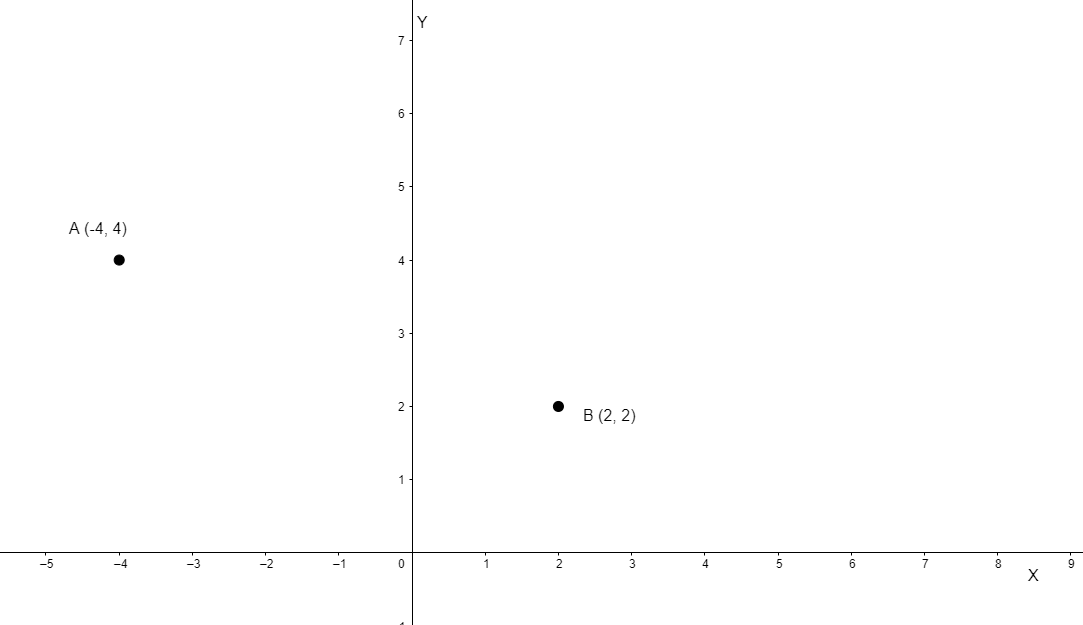
(i) Here, we have to plot points A (– 4, 4) and B (2, 2)

Since x – coordinate of A is negative and y – coordinate is positive, therefore point A will lie in the second quadrant. Now, both x and y – coordinates of B are positive, so point B lies in the first quadrant. So, the graph can be plotted as

(ii) Here, we have to reflect the points A and B in the origin to obtain points A’ and B’ respectively. Now, to reflect the point in the origin we first reflect it in the y – axis, and then this reflected point is again reflected in the x-axis. So, let us reflect on both points one by one.
(a) For point A (– 4, 4):
When we will reflect this point in the y – axis then its x – coordinate will become 4 and the y – coordinate will remain unchanged. So, the point will become (4, 4). Now, when (4, 4) is reflected in the x-axis then its y – coordinate will become – 4 and x – coordinate will remain unchanged. So, the coordinates of A’ will be (4, – 4).
(b) For point B (2, 2):
When we will reflect this point in the y – axis then its x – coordinate will become – 2 and the y – coordinate will remain unchanged. So, the point will become (– 2, 2). Now, when (– 2, 2) is reflected in the x-axis then its y- coordinate will be – 2 and x – coordinate will remain unchanged. So, the coordinates of B’ will be (– 2, – 2). So, the graph can be plotted as

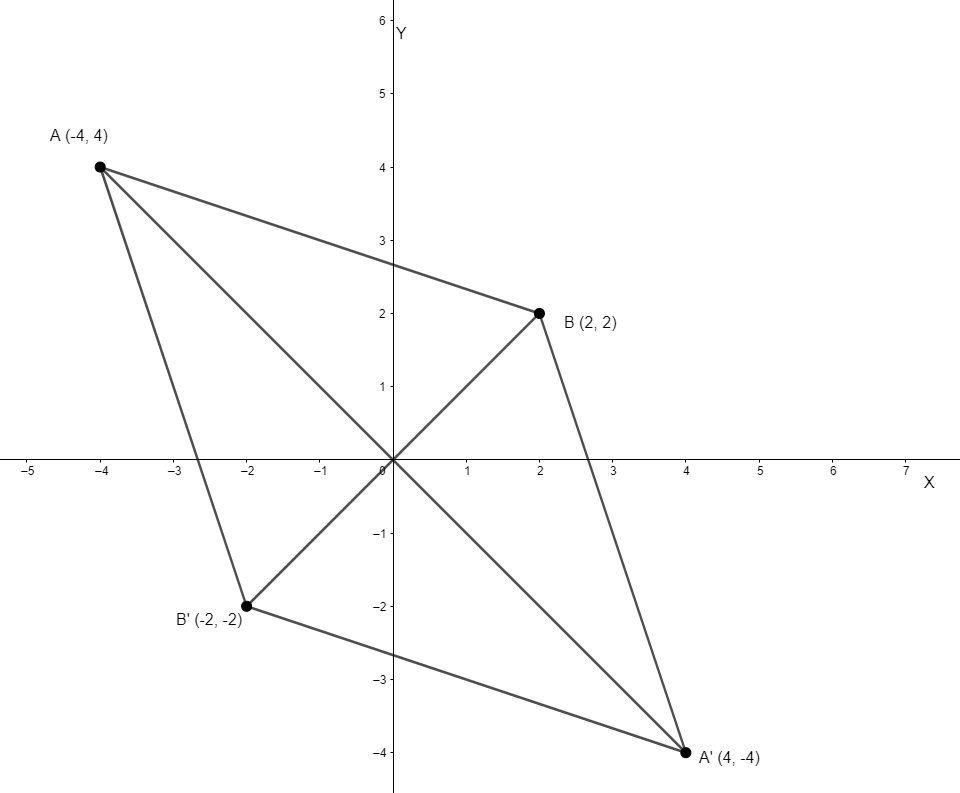
(iii) The coordinates of A’ and B’ are (4, – 4) and (– 2, – 2) respectively.
(iv) Here, we have to give the geometrical name for the figure ABA’B’.
Clearly, we can see that the opposite sides of the quadrilateral obtained are parallel to each other. Now, apply the distance formula given as \[d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}},\] where d is the distance to find the length of the sides, we get,
\[\Rightarrow AB=\sqrt{{{\left( -4-2 \right)}^{2}}+{{\left( 4-2 \right)}^{2}}}=\sqrt{40}=2\sqrt{10}\text{ units}\]
\[\Rightarrow B{{A}^{'}}=\sqrt{{{\left( 2-4 \right)}^{2}}+{{\left( 2-\left( -4 \right) \right)}^{2}}}=\sqrt{40}=2\sqrt{10}\text{ units}\]
\[\Rightarrow {{A}^{'}}{{B}^{'}}=\sqrt{{{\left( 4-\left( -2 \right) \right)}^{2}}+{{\left( -4-\left( -2 \right) \right)}^{2}}}=\sqrt{40}=2\sqrt{10}\text{ units}\]
\[\Rightarrow {{B}^{'}}{{A}^{'}}=\sqrt{{{\left( -2-\left( -4 \right) \right)}^{2}}+{{\left( -2-\left( -4 \right) \right)}^{2}}}=\sqrt{40}=2\sqrt{10}\text{ units}\]
So, all the sides of the quadrilateral are equal to each other.
Hence, we can conclude that ABA’B’ is a rhombus.
(v) Here, we have to name and draw the lines of symmetry of ABA’B’.
Now, we know that the two diagonals cut a rhombus into two equal halves. So, these diagonals are the only two lines of symmetry of rhombus ABA’B’. It is shown in the figure drawn in part of the above solution. So, we have,
Lines of symmetry = AA’ and BB’

Note:
One may note that while reflecting the points A’ and B’ in the origin, we reflected these points in the y – axis first and then in the x-axis. You may also interchange this reflection process. It will not alter the coordinates. Remember the properties of basic shapes like square, rectangle, rhombus, and parallelogram to determine the quadrilateral obtained. One can also remember a short method to reflect the point in the origin, that is the numerical value of the coordinate remains the same and only the sign gets reversed of the final reflected point.