Question

Using Cauchy’s mean value theorem, prove that $\dfrac{\sin \alpha -\sin \beta }{\cos \beta -\cos \alpha }=\cot \theta $ where $0<\alpha <\theta <\beta <\dfrac{\pi }{2}$.

Answer 1

Hint: To solve this question, we should know the Cauchy theorem. Let us consider two functions $f\left( x \right)$and $g\left( x \right)$ which are continuous in the interval $\left[ a,b \right]$ and differentiable in the interval $\left( a,b \right)$ and $g\left( b \right)\ne g\left( a \right),g'\left( x \right)\ne 0\forall \left( a,b \right)$. We can write that there exist at least one value of $c$ which satisfies the equation $\dfrac{f\left( b \right)-f\left( a \right)}{g\left( b \right)-g\left( a \right)}=\dfrac{f'\left( c \right)}{g'\left( c \right)}$. In our question, by considering $f\left( x \right)=\sin x,g\left( x \right)=\cos x$ , $\left( a,b \right)=\left( \alpha ,\beta \right)$ and $c=\theta $, we get the answer.

Complete step by step answer:
We are asked to prove the equation $\dfrac{\sin \alpha -\sin \beta }{\cos \beta -\cos \alpha }=\cot \theta $ where $0<\alpha <\theta <\beta <\dfrac{\pi }{2}$. For this question, we should use Cauchy’s mean value theorem.
Let us consider two functions $f\left( x \right)$and $g\left( x \right)$ which are continuous in the interval $\left[ a,b \right]$ and differentiable in the interval $\left( a,b \right)$ and $g\left( b \right)\ne g\left( a \right),g'\left( x \right)\ne 0\forall \left( a,b \right)$. We can write that there exist at least one value of $c$ which satisfies the equation $\dfrac{f\left( b \right)-f\left( a \right)}{g\left( b \right)-g\left( a \right)}=\dfrac{f'\left( c \right)}{g'\left( c \right)}$.
This is the statement of Cauchy’s mean value theorem.
Let us consider $f\left( x \right)=\sin x$ and $g\left( x \right)=\cos x$. We know that $\sin x,\cos x$ are continuous and differentiable everywhere in the real domain. So, the assumed functions are continuous and differentiable in the range $\left( \alpha ,\beta \right)$. So, we can apply the Cauchy’s mean value theorem for the given range.
We can write that $f\left( x \right)=\sin x,g\left( x \right)=\cos x$, $\left( a,b \right)=\left( \alpha ,\beta \right)$ and $c=\theta $. We know that $\alpha \ne \beta \Rightarrow \cos \alpha \ne \cos \beta $ and $\sin \theta \ne 0$ in the given range.


By applying the mean value theorem, we get
$\begin{align}
  & \dfrac{\sin \beta -\sin \alpha }{\cos \beta -\cos \alpha }=\dfrac{d{{\left( \sin x \right)}_{\theta }}}{d{{\left( \cos x \right)}_{\theta }}} \\
 & \dfrac{\sin \beta -\sin \alpha }{\cos \beta -\cos \alpha }=\dfrac{\cos \theta }{-\sin \theta } \\
 & \dfrac{\sin \beta -\sin \alpha }{\cos \beta -\cos \alpha }=-\cot \theta \\
\end{align}$
Multiplying by $-1$ on both sides, we get
\[\begin{align}
  & -1\left( \dfrac{\sin \beta -\sin \alpha }{\cos \beta -\cos \alpha } \right)=-1\left( -\cot \theta \right) \\
 & \dfrac{\sin \alpha -\sin \beta }{\cos \beta -\cos \alpha }=\cot \theta \\
\end{align}\]
$\therefore $Hence, we proved the required equation.

Note:
While solving questions using any of the mean value theorems, the initial conditions play a major role. Every condition of the theorem should be satisfied in order to apply the theorem or else we will end up getting the wrong results. The graphical representation of the Cauchy’s mean value theorem is

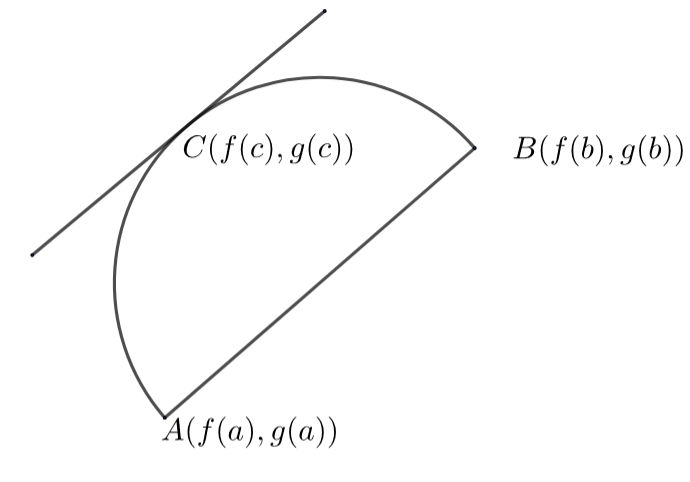
We can see that the slope of the line AB is equal to the slope of the tangent at C to the curve. The equality of slopes is what actually explained in the mean value theorem.