
Using a protractor, draw an angle of measure ${108^ \circ }$. With this angle as given, draw an angle of ${54^ \circ }$.
Answer
603.6k+ views
Hint: Start by drawing the given angle of ${108^ \circ }$ using protractor, the next step is to analyse the next angle they have given us to draw, in this question they have given us ${54^ \circ }$ which is just the half of ${108^ \circ }$, so we can bisect the angle. To bisect the angle, we take radius in the compass and draw the arc from x axis and y axis, the point at which they intersect is the point where ${54^ \circ }$ is obtained, from the origin extending a line to that point.
Complete step-by-step answer:
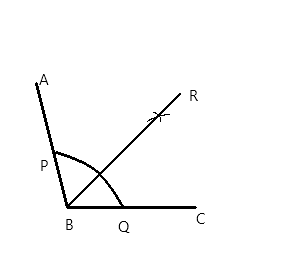
Step #1: Using protractor, draw an angle ABC of measure ${108^ \circ }$
Step #2: With centre B, and taking any radius, draw an arc, intersecting the ray BA and the ray BC at point D and E respectively.
Step #3: With centre D and radius greater than half of DE, draw an arc inside the angle.
Step #4: With centre E and taking the same radius as in step 3, draw an arc intersecting the arc drawn in step 3, at F.
Step #5: Draw the ray BF. This is the angle bisector of angle ABC. So $\angle FBC = {54^ \circ }$
Step #6: With centre B and taking any radius, draw an arc intersecting the ray BF and the ray BC at G and H respectively.
Step #7: Draw a ray MN.
Step #8: With a centre M and taking the same radius as in step 6, draw an arc intersecting the ray MN at point P.
Step #9: With centre P and taking radius equal to HG, draw an arc intersecting the arc drawn in step 8, at point L.
Step #10: Draw the ray ML.
Angle LMN is the desired angle of measure ${54^ \circ }$
Note: The main motive in this question should be o understand the relation between the angles given to draw, like in this question one of the angle was half the angle that was given, therefore we bisected it once, similarly if they had given us an angle one-third the given angle then we should have bisected it thrice, and so on.
Complete step-by-step answer:
Step #1: Using protractor, draw an angle ABC of measure ${108^ \circ }$
Step #2: With centre B, and taking any radius, draw an arc, intersecting the ray BA and the ray BC at point D and E respectively.
Step #3: With centre D and radius greater than half of DE, draw an arc inside the angle.
Step #4: With centre E and taking the same radius as in step 3, draw an arc intersecting the arc drawn in step 3, at F.
Step #5: Draw the ray BF. This is the angle bisector of angle ABC. So $\angle FBC = {54^ \circ }$
Step #6: With centre B and taking any radius, draw an arc intersecting the ray BF and the ray BC at G and H respectively.
Step #7: Draw a ray MN.
Step #8: With a centre M and taking the same radius as in step 6, draw an arc intersecting the ray MN at point P.
Step #9: With centre P and taking radius equal to HG, draw an arc intersecting the arc drawn in step 8, at point L.
Step #10: Draw the ray ML.
Angle LMN is the desired angle of measure ${54^ \circ }$

Note: The main motive in this question should be o understand the relation between the angles given to draw, like in this question one of the angle was half the angle that was given, therefore we bisected it once, similarly if they had given us an angle one-third the given angle then we should have bisected it thrice, and so on.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Who was the first woman to receive Bharat Ratna?

Write a letter to the principal requesting him to grant class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Discuss the main reasons for poverty in India




