Question

How do you use the law of sines to solve the triangle given \[A=71{}^\circ \], a=9.3, b=8.5?

Answer 1

Hint: This question is from the topic of trigonometry. In this question, we will find the other parameters of the triangle using the given parameters. We will use the sine rule formula in this question to solve the problem. We will understand this question by using some figures.

Complete step by step answer:
Let us solve this question.
In this question, we have asked to use the law of sines and solve the triangle by using parameters. Or, we can say that we have to find the other parameters of the triangle using the given parameters of the triangle. The given parameters are:
\[A=71{}^\circ \], a=9.3, b=8.5
So, we have to find the other two angles of the triangle and the third side of the triangle.
So, let us understand this from the following figure:

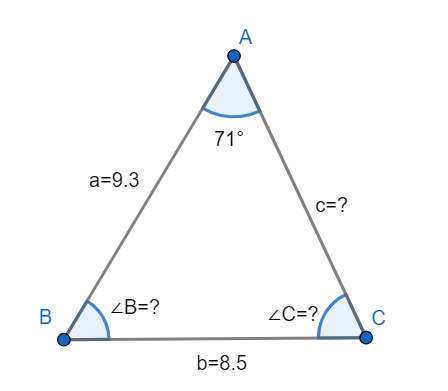
So, we can say that we have to find the value of length c and the values of angle B and angle C.
Now, let us understand the sine rule or we can say law of sines from the following figure:

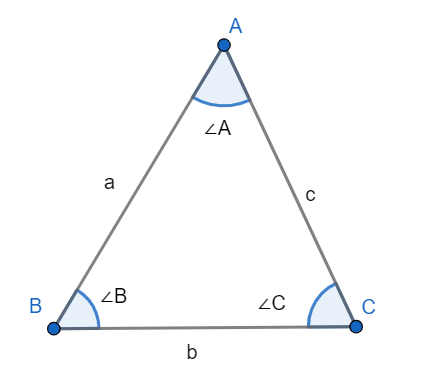
The sine rule is:
\[\dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c}\]
So, using the above formula, we can write
\[\dfrac{\sin 71{}^\circ }{9.3}=\dfrac{\sin B}{8.5}=\dfrac{\sin C}{c}\]
The above can also be written as
\[\Rightarrow \dfrac{\sin 71{}^\circ }{9.3}=\dfrac{\sin B}{8.5}\]
From the above, we can write
\[\Rightarrow \sin B=\dfrac{\sin 71{}^\circ }{9.3}\times 8.5\]
\[\Rightarrow \sin B=\dfrac{0.95}{9.3}\times 8.5\]
\[\Rightarrow \sin B=0.868\]
Taking inverse, we can write
\[\Rightarrow B={{\sin }^{-1}}0.868\]
The above can also be written as
\[\Rightarrow B=60{}^\circ \]
Hence, we got that angle B is 60 degrees.
And, we know that the sum of all angles of a triangle is always 180 degrees. So, we can write
\[A+B+C=180{}^\circ \]
Using the value of A and B, we can write
\[\Rightarrow 71{}^\circ +60{}^\circ +C=180{}^\circ \]
The above can also be written as
\[\Rightarrow 131{}^\circ +C=180{}^\circ \]
\[\Rightarrow C=180{}^\circ -131{}^\circ =49{}^\circ \]
Hence, we got that the angle C is 49 degrees.
Now, using the formula \[\dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c}\], let us find the value of c.
We can write
\[\dfrac{\sin 71{}^\circ }{9.3}=\dfrac{\sin C}{c}\]
The above can also be written as
\[\Rightarrow \dfrac{\sin 71{}^\circ }{9.3}=\dfrac{\sin 49{}^\circ }{c}\]
\[\Rightarrow c=\dfrac{\sin 49{}^\circ }{\sin 71{}^\circ }\times 9.3\]
The above can also be written as
\[\Rightarrow c=\dfrac{0.754}{0.945}\times 9.3\]
\[\Rightarrow c=7.42\]
Hence, we have solved the triangle using the law of sines.
We can understand from the following figure:

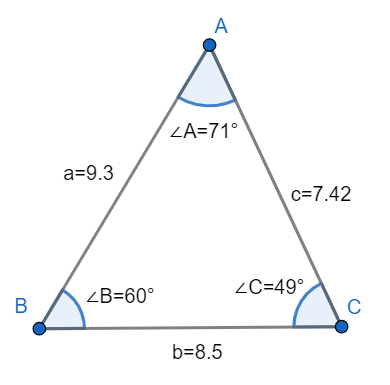
Note: We should have better knowledge in the topic of triangles to solve this type of question easily. We should know about the sine rule or law of sines. We can understand this from the following:
\[\dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c}\]

We should know that the sum of interior angles of the triangle is always 180 degrees.