Question

Use ruler and compass only for the following question. All construction lines and arcs must be clearly shown.
Construct a $\vartriangle ABC$ in which BC = 6.5 cm,$\angle ABC=60{}^\circ $, AB = 5 cm. Construct a locus of points ${{l}_{1}}$ at a distance of 3.5 cm from A. Also, construct a locus of points ${{l}_{2}}$ which is equidistant from AC and BC. Let ${{l}_{1}}$ intersect ${{l}_{2}}$ in two points X and Y. Measure XY.

Answer 1

Hint: In this problem, we are to follow the given instructions and draw a figure. We will start off with drawing the base of a triangle which is 6.5 cm. Then by using the given angles we can get our desired triangle. Now, the easiest way to find the equidistant points is to draw a circle around it so that the radius gives us the needed points. And then we draw the bisector of the angle ACB and thus we get X and Y points. Measuring XY we are getting the needed answer.

Complete step-by-step solution:
We start with, drawing the base BC = 6.5 cm.

Now we are drawing an angle of 60 degrees from B.

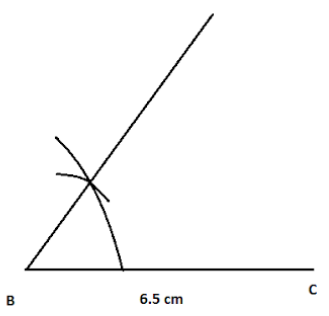
Now, we will try to draw an arc of radius 5 cm from B on the 60 degree angle and will name it as A. Then, we will join A and C. Thus, we get ABC, which is our required triangle.

For the second part, we will start with, drawing a circle putting the radius 3.5 cm and as centre A, so that the locus takes place equidistant from the origin.
Thus, we have,

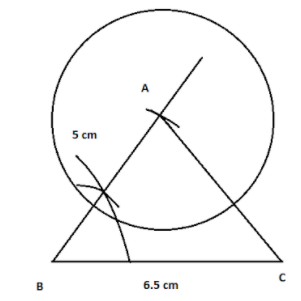
Now, to find the points equidistant from AC and BC, we are to draw the angle bisector of angle ACB, which will give us the locus of the points.
So, we get now,

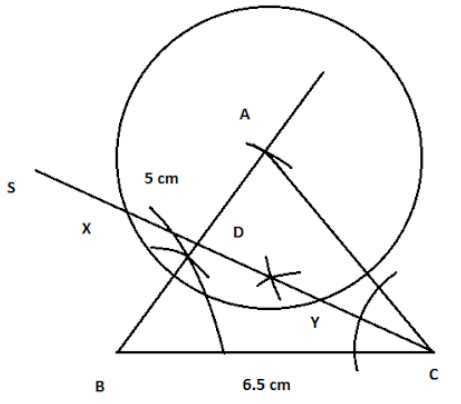
By measuring XY, we are getting that XY = 5 cm.

Note: In this type of given problems, it is necessary to name the points and act accordingly. The questions should be carefully read and then using the proper instructions we should reach the figure we need. One wrong step can get the whole answer into doubt.