Question

Two trees, A and B are on the same side of a river. From a point C in the river the distance of the tree A and B is 250 m and 300 m respectively. If the angle C is ${45^0}$, find the distance between the trees (use $\sqrt 2 = 1.44$).

Answer 1

Hint- Here, we are given two sides and one interior angle of a triangle ABC and we have to find the third side of this triangle. This can be also done by using the cosine rule in the triangle ABC which is ${\left( {{\text{AB}}} \right)^2} = {\left( {{\text{AC}}} \right)^2} + {\left( {{\text{BC}}} \right)^2} - 2\left( {{\text{AC}}} \right)\left( {{\text{BC}}} \right)\cos \left( {\angle {\text{C}}} \right)$


Complete step-by-step solution -

Let us draw a triangle ABC with points A and B representing two trees on the same side of the river and C is a point in the river as shown in the figure.

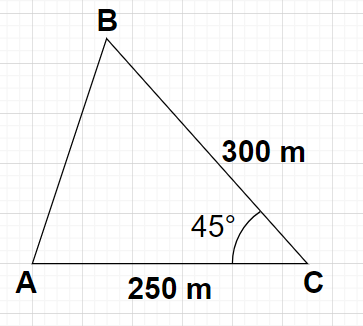
Given, AC = 250 m, BC = 300 m, $\angle {\text{C}} = {45^0}$
According to cosine rule (for the length AB) applied on any triangle ABC, we can write
${\left( {{\text{AB}}} \right)^2} = {\left( {{\text{AC}}} \right)^2} + {\left( {{\text{BC}}} \right)^2} - 2\left( {{\text{AC}}} \right)\left( {{\text{BC}}} \right)\cos \left( {\angle {\text{C}}} \right){\text{ }} \to {\text{(1)}}$
By substituting AC = 250, BC = 300 and $\angle {\text{C}} = {45^0}$ in equation (1), we get
$ \Rightarrow {\left( {{\text{AB}}} \right)^2} = {\left( {{\text{250}}} \right)^2} + {\left( {{\text{300}}} \right)^2} - 2\left( {{\text{250}}} \right)\left( {{\text{300}}} \right)\cos \left( {{{45}^0}} \right){\text{ }} \to {\text{(2)}}$
According to the general trigonometric table,
$\cos {45^0} = \dfrac{1}{{\sqrt 2 }}{\text{ }} \to {\text{(3)}}$
By substituting equation (3) in equation (2), we get
$ \Rightarrow {\left( {{\text{AB}}} \right)^2} = 62500 + 90000 - 150000\left( {\dfrac{1}{{\sqrt 2 }}} \right)$
Using $\sqrt 2 = 1.44$, the above equation becomes
$
  {\left( {{\text{AB}}} \right)^2} = 62500 + 90000 - 150000\left( {\dfrac{1}{{1.44}}} \right) \\
   \Rightarrow {\left( {{\text{AB}}} \right)^2} = 62500 + 90000 - \dfrac{{312500}}{3} \\
   \Rightarrow {\left( {{\text{AB}}} \right)^2} = 62500 + 90000 - \dfrac{{312500}}{3} \\
   \Rightarrow {\left( {{\text{AB}}} \right)^2} = \dfrac{{145000}}{3} \\
 $
By taking square root on both sides of the above equation, we get
$ \Rightarrow {\text{AB}} = \sqrt {\dfrac{{145000}}{3}} = 219.85{\text{ m}}$
Therefore, the distance between the trees A and B is 219.85 m

Note- In general, there are three cosine rules which can be applied in any triangle ABC. The length AB is given by ${\left( {{\text{AB}}} \right)^2} = {\left( {{\text{AC}}} \right)^2} + {\left( {{\text{BC}}} \right)^2} - 2\left( {{\text{AC}}} \right)\left( {{\text{BC}}} \right)\cos \left( {\angle {\text{C}}} \right)$, the length BC is given by \[{\left( {{\text{BC}}} \right)^2} = {\left( {{\text{AB}}} \right)^2} + {\left( {{\text{AC}}} \right)^2} - 2\left( {{\text{AB}}} \right)\left( {{\text{AC}}} \right)\cos \left( {\angle {\text{A}}} \right)\] and the length AC is given by \[{\left( {{\text{AC}}} \right)^2} = {\left( {{\text{AB}}} \right)^2} + {\left( {{\text{BC}}} \right)^2} - 2\left( {{\text{AB}}} \right)\left( {{\text{BC}}} \right)\cos \left( {\angle {\text{B}}} \right)\].