Question

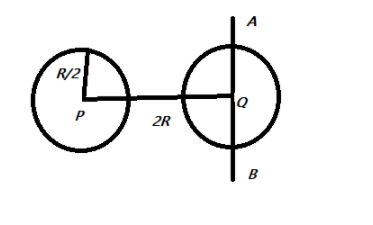
Two spheres each of mass $M$ and radius $\dfrac{R}{2}$ are connected with a massless rod of length \[2R\] as shown in the figure. What will be the moment of inertia of the system about an axis passing through the centre of one of the spheres and perpendicular to the rod:

\[\begin{align}
  & A.\dfrac{21}{5}M{{R}^{2}} \\
 & B.\dfrac{2}{5}M{{R}^{2}} \\
 & C.\dfrac{5}{2}M{{R}^{2}} \\
 & D.\dfrac{5}{21}M{{R}^{2}} \\
\end{align}\]

Answer 1

Hint: Moment of inertia is the property of a body to resist angular acceleration. It is also the sum of the product of the masses of every particle with the square of the distances from the chosen axis of rotation. It is also known as the angular mass or rotational inertia.

Formula used:
 $I=mr^{2}$

Complete step-by-step answer:
Given, that the mass of the spheres is $M$ and the radius is $\dfrac{R}{2}$, also if they are separated by a distance \[2R\]
To find the moment of inertia of the system we need to use the parallel axis theorem of the moment of inertia. Which states that, if $M$ mass of a body is rotated along the axis of the centre of mass of the body, then the new axis, which is parallel to the axis of rotation and at a distance say $d$, then the moment of inertia along the new axis $I_{new}$ is given as the sum of moment of inertia along the old axis and the product of the mass of the body with the distance between the two axis .
Or, $I_{new}=I+Md^{2}$
Let us first find the inertia of the individual system.
We know that the moment of inertia of sphere with centre $P$ along \[AB\] is given by $I_{P}=\dfrac{2}{5}M\left(\dfrac{R}{2}\right)^{2}=\dfrac{1}{10}MR^{2}$
Similarly, the moment of inertia of sphere with centre $Q$ along \[AB\] is given by $I_{Q}=\dfrac{2}{5}M\left(\dfrac{R}{2}\right)^{2}=\dfrac{1}{10}MR^{2}$
Using parallel axis theorem, we get,
$I_{new}=I_{P}+I_{Q}+Md^{2}$
Here $d=2R$
The, $I_{new}=\dfrac{1}{10}MR^{2}+\dfrac{1}{10}MR^{2}+M(2R)^{2}$
Or, $I_{new}=\dfrac{1}{5}MR^{2}+4MR^{2}$
Or, $I_{new}=\dfrac{1+20}{5}MR^{2}$
Or, $I_{new}=\dfrac{21}{5}MR^{2}$

So, the correct answer is “Option A”.

Note: The moment of inertia depends on the density of the material, the axis of rotation and the dimensions of the body, i.e. the shape and the size of the body. Its dimensional formula is given as $[M^{1}L^{2}T^{0}]$ with SI unit is $kgm^{2}$.