Question

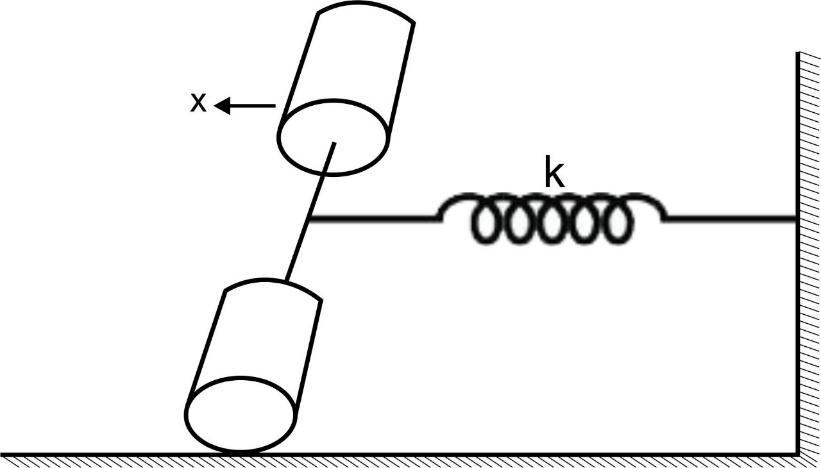
Two solid cylinders connected with a short light rod about common axis have radius $ R $ and total mass $ M $ rest on a horizontal tabletop connected to a spring of spring constant $ k $ as shown. The cylinders are pulled to the left by x and released. There is sufficient friction for the cylinders to roll. Find the time period of oscillation?

(A) $ 2\pi \sqrt {\dfrac{M}{k}} $
(B) $ 2\pi \sqrt {\dfrac{M}{{2k}}} $
(C) $ 2\pi \sqrt {\dfrac{{3M}}{{2k}}} $
(D) $ 2\pi \sqrt {\dfrac{M}{{3k}}} $

Answer 1

Hint
In this question, apply the concept of the force equilibrium equation along the horizontal direction to obtain the result. First write the torque equilibrium equation to obtain the expression for the frictional force applied on the cylinder, then apply the dynamic force equilibrium equation to obtain the expression for the time period of the oscillat

Complete step by step answer
In this question, two solid cylinders are connected by a rod and the total mass of the system is $ M $ . The system is connected to a spring whose spring constant is $ k $ and rested on the horizontal top table. The friction force needs to be considered and if the cylinders are pulled to the left by $ x $ amount, the time period of the oscillation needs to be calculated.
As we know that the motion is pure rolling t, so the rotational inertia is given as,
 $ I = \dfrac{1}{2}M{R^2}......\left( 1 \right) $
Here, the moment of inertia is $ I $ .
Now apply the Newton’s second law for angular motion to obtain the following equation,
 $ \sum \tau = I\alpha
  \tau = I\alpha ......\left( 2 \right) $
Here, the torque applied on the cylinders is $ \tau $ and the angular acceleration of the cylinder is $ \alpha $ .
Now, we write the equation of the torque applied on the cylinder due to friction,
 $ \tau = {f_s}R......\left( 3 \right) $
Here the friction force applied on the cylinder is $ {f_s} $ .
Now substituting (3) and (1) in equation (2) as shown below:
 $ {f_s}R = \dfrac{1}{2}M{R^2}\alpha $
By simplifying the above equation, we get,
 $ \Rightarrow {f_s} = \dfrac{1}{2}MR\alpha $
As we know that linear and angular acceleration can be written as,
 $ a = R\alpha $
Now, apply the force equilibrium equation that is the forces acting on the system are frictional and spring force,
 $ \sum F = fs - kx $
After simplification, we get,
 $ \Rightarrow Ma = fs - kx $
Now, by substituting the derived equation of acceleration, friction force in the above equation we get,
 $ Ma = - fs + kx $
 $ \Rightarrow M\left( {R\alpha } \right) = - \dfrac{1}{2}MR\alpha + kx $
By simplifying the above equation,
 $ \Rightarrow \dfrac{3}{2}M\left( {R\alpha } \right) = kx $
As we know that $ a = R\alpha $ , substitute $ a $ in place of $ R\alpha $ as,
 $ \Rightarrow \dfrac{3}{2}M\left( a \right) = kx $
Now, simplifying it further,
 $ \Rightarrow a = \dfrac{{2k}}{{3M}}x......\left( 4 \right) $
As we know that,
 $ a = {\omega ^2}x......\left( 5 \right) $
Where, $ \omega $ is the angular velocity.
Now, compare equation (4) and (5), we get
 $ {\omega ^2} = \dfrac{{2k}}{{3M}} $
Simplify further,
 $ \Rightarrow \omega = \sqrt {\dfrac{{2k}}{{3M}}} $
Since, $ T = \dfrac{{2\pi }}{\omega } $ and $ \omega = \sqrt {\dfrac{{2k}}{{3M}}} $
Substituting the value of $ \omega $ in $ T = \dfrac{{2\pi }}{\omega } $ we get the value of time period of oscillation as
 $ \therefore T = 2\pi \sqrt {\dfrac{{3M}}{{2k}}} $
Therefore, the correct option is (C).

Note
Be careful about the sign convention of the friction and the spring force applied on the cylinder. We can also calculate the frequency of the oscillation as we know that the frequency is the reciprocal of the time period.