Question

Two small balls having equal positive charge Q (coulomb) on each are suspended by two insulating strings of equal length L, from a hook fixed to a stand. If the whole set up is taking in a satellite then the angle $\theta $ between the two strings is: (in equilibrium).
$\left( A \right){0^0}$
$\left( B \right){90^0}$
$\left( C \right){180^0}$
$\left( D \right){0^0} < \theta < {180^0}$

Answer 1

Hint: In this question use the concept that in a satellite the acceleration due to gravity becomes zero so the weight of the system becomes zero and use the concept that two like charges repel each other so use these properties to reach the solution of the question.

Complete Step-by-Step solution:

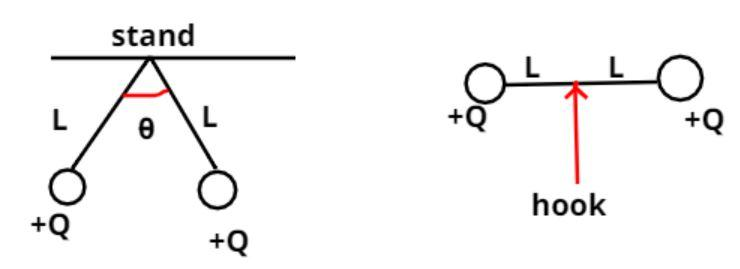
The pictorial representation of the above problem is shown above when we have on the earth surface the system represented as figure 1 having angle $\theta $ between two strings each of length L as shown in the figure.
But when we placed this system into the satellite the acceleration due to gravity becomes zero so the force acting on two small balls becomes zero as (F = ma) acceleration is zero so force is zero.
So the two balls fell zero weight in the satellite.
Now it is given that these two spherical balls have equal positive charge Q as shown in the figure so they both feel electrostatic force of repulsion as like force repel each other so the string becomes horizontal and the angle between these two strings becomes a straight angle, as shown in figure 2.
And we all know straight angle = ${180^0}$
Hence option (C) is the correct answer.

Note – If the charges on the balls are opposite to each other i.e. equal but opposite in sign so they feel electrostatic force of attraction as unlike charges attract each other so they overlap each other and the angle between the strings become zero degree.