Question

Two slits at a distance of 1mm are illuminated by a light of wave length $6.5\times {{10}^{-7}}m$. The interference fringes are observed on a screen placed at a distance of 1m. The interference between the third dark fringe and the fifth bright fringe will be
a) 0.65cm
b) 4.8mm
c) 1.625mm
d) 3.25cm

Answer 1

Hint: The interference pattern on the screen will be of the form alternate bright and the dark fringes. The slit separation, the wavelength of light used as well as the distance of the slit to the screen is given to us. Therefore we will use the condition of the bright and the dark fringe to determine the position of the fifth bright and the third dark fringe in order to determine the distance between them.
Formula used:
${{x}_{N}}(bright)=\dfrac{n\lambda D}{d}$
${{x}_{N}}(dark)=\dfrac{(2N-1)\lambda D}{2d}$

Complete answer:

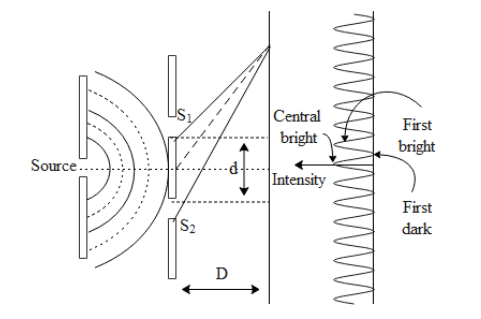
In the above figure we can see how the interference pattern is observed on the screen placed at a distance D from the two slits. In the above question it is given to us that slit separation d=1mm, wavelength of the light incident on the slits is $6.5\times {{10}^{-7}}m$ and the distance of separation between the slits and the screen i.e. D= 1m. The position of the ${{N}^{th}}$ bright fringe with respect to the centre of the central bright fringe is given by,
${{x}_{N}}(bright)=\dfrac{n\lambda D}{d}$
Similarly the position of the ${{N}^{th}}$ dark fringe with respect to the centre of the central bright fringe is given by,
${{x}_{N}}(dark)=\dfrac{(2N-1)\lambda D}{2d}$
From the above equation the position of the fifth bright fringe we get equal to,
$\begin{align}
  & {{x}_{N}}(bright)=\dfrac{n\lambda D}{d} \\
 & \Rightarrow {{x}_{5}}(bright)=\dfrac{5\times 6.7\times {{10}^{-7}}m\times 1m}{1mm} \\
 & \Rightarrow {{x}_{5}}(bright)=\dfrac{5\times 6.7\times {{10}^{-7}}\times 1}{1\times {{10}^{-3}}}m \\
 & \Rightarrow {{x}_{5}}(bright)=32.5\times {{10}^{-4}}m \\
\end{align}$
Similarly, from the equation of dark fringe position of the third dark fringe we get equal to,
$\begin{align}
  & {{x}_{N}}(dark)=\dfrac{(2N-1)\lambda D}{2d} \\
 & \Rightarrow {{x}_{3}}(dark)=\dfrac{(2\left( 3 \right)-1)\times 6.7\times {{10}^{-7}}m\times 1m}{2mm} \\
 & \Rightarrow {{x}_{3}}(dark)=\dfrac{5\times 6.7\times {{10}^{-7}}\times 1}{2\times {{10}^{-3}}}m \\
 & \Rightarrow {{x}_{3}}(dark)=16.25\times {{10}^{-4}}m \\
\end{align}$
Since both are located from the central bright fringe, the distance(X) between them is ,
$\begin{align}
  & X={{x}_{5}}(bright)-{{x}_{3}}(dark) \\
 & \Rightarrow X=32.5\times {{10}^{-4}}-16.25\times {{10}^{-4}} \\
 & \Rightarrow X=1.625\times {{10}^{-3}}m=1.625mm \\
\end{align}$

Hence the correct answer of the above question is option c.

Note:
It is to be noted we always have a central bright fringe. After that we get an alternating pattern of dark and bright fringes. It is to be noted that in case of interference the intensity of the dark and the bright fringes remains constant whereas in case of diffraction it’s not.